Algebra: Ratio Word Problems
Related Pages Two-Term Ratio Word Problems More Ratio Word Problems Algebra Lessons
In these lessons, we will learn how to solve ratio word problems that have two-term ratios or three-term ratios.
Ratio problems are word problems that use ratios to relate the different items in the question.
The main things to be aware about for ratio problems are:
- Change the quantities to the same unit if necessary.
- Write the items in the ratio as a fraction .
- Make sure that you have the same items in the numerator and denominator.
Printable Introduction to Ratios
Ratio Word Problems using Tape diagrams Ratio Problems given One of Quantities Ratio Problems given Total Ratio Problems given Difference Ratio Problems with Change of Ratio
Online Ratio of Quantities Ratio Word Problems I Ratio Word Problems II Ratio Word Problems III Ratio Word Problems IV Ratio with Algebra

Ratio Problems: Two-Term Ratios
Example 1: In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there?
Solution: Step 1: Assign variables: Let x = number of red sweets.
Step 2: Solve the equation. Cross Multiply 3 × 120 = 4 × x 360 = 4 x
Answer: There are 90 red sweets.
Example 2: John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane?
Solution: Step 1: Sentence: Jane has 20 marbles, all of them either red or blue. Assign variables: Let x = number of blue marbles for Jane 20 – x = number red marbles for Jane
Step 2: Solve the equation
Cross Multiply 3 × x = 2 × (20 – x ) 3 x = 40 – 2 x
John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane.
Answer: John has 4 more blue marbles than Jane.
How To Solve Word Problems Using Proportions?
This is another word problem that involves ratio or proportion.
Example: A recipe uses 5 cups of flour for every 2 cups of sugar. If I want to make a recipe using 8 cups of flour. How much sugar should I use?
How To Solve Proportion Word Problems?
When solving proportion word problems remember to have like units in the numerator and denominator of each ratio in the proportion.
- Biologist tagged 900 rabbits in Bryer Lake National Park. At a later date, they found 6 tagged rabbits in a sample of 2000. Estimate the total number of rabbits in Bryer Lake National Park.
- Mel fills his gas tank up with 6 gallons of premium unleaded gas for a cost of $26.58. How much would it costs to fill an 18 gallon tank? 3 If 4 US dollars can be exchanged for 1.75 Euros, how many Euros can be obtained for 144 US dollars?
Ratio problems: Three-term Ratios
Example 1: A special cereal mixture contains rice, wheat and corn in the ratio of 2:3:5. If a bag of the mixture contains 3 pounds of rice, how much corn does it contain?
Solution: Step 1: Assign variables: Let x = amount of corn
Step 2: Solve the equation Cross Multiply 2 × x = 3 × 5 2 x = 15
Answer: The mixture contains 7.5 pounds of corn.
Example 2: Clothing store A sells T-shirts in only three colors: red, blue and green. The colors are in the ratio of 3 to 4 to 5. If the store has 20 blue T-shirts, how many T-shirts does it have altogether?
Solution: Step 1: Assign variables: Let x = number of red shirts and y = number of green shirts
Step 2: Solve the equation Cross Multiply 3 × 20 = x × 4 60 = 4 x x = 15
5 × 20 = y × 4 100 = 4 y y = 25
The total number of shirts would be 15 + 25 + 20 = 60
Answer: There are 60 shirts.
Algebra And Ratios With Three Terms
Let’s study how algebra can help us think about ratios with more than two terms.
Example: There are a total of 42 computers. Each computer runs one of three operating systems: OSX, Windows, Linux. The ratio of the computers running OSX, Windows, Linux is 2:5:7. Find the number of computers that are running each of the operating systems.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
- Math Article
- Ratios And Proportion
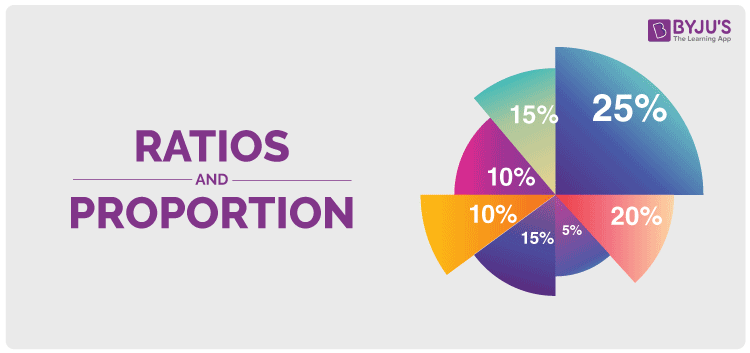
Ratios and Proportion

Ratio and Proportion are explained majorly based on fractions. When a fraction is represented in the form of a:b, then it is a ratio whereas a proportion states that two ratios are equal. Here, a and b are any two integers. The ratio and proportion are the two important concepts, and it is the foundation to understand the various concepts in mathematics as well as in science.

In our daily life, we use the concept of ratio and proportion such as in business while dealing with money or while cooking any dish, etc. Sometimes, students get confused with the concept of ratio and proportion. In this article, the students get a clear vision of these two concepts with more solved examples and problems.
For example, ⅘ is a ratio and the proportion statement is 20/25 = ⅘. If we solve this proportional statement, we get:
20 x 5 = 25 x 4
Check: Ratio and Proportion PDF
Therefore, the ratio defines the relationship between two quantities such as a:b, where b is not equal to 0. Example: The ratio of 2 to 4 is represented as 2:4 = 1:2. And the statement is said to be in proportion here. The application of proportion can be seen in direct proportion .
What is Ratio and Proportion in Maths?
The definition of ratio and proportion is described here in this section. Both concepts are an important part of Mathematics. In real life also, you may find a lot of examples such as the rate of speed (distance/time) or price (rupees/meter) of a material, etc, where the concept of the ratio is highlighted.
Proportion is an equation that defines that the two given ratios are equivalent to each other. For example, the time taken by train to cover 100km per hour is equal to the time taken by it to cover the distance of 500km for 5 hours. Such as 100km/hr = 500km/5hrs.
Let us now learn Maths ratio and proportion concept one by one.
Ratio Meaning
In certain situations, the comparison of two quantities by the method of division is very efficient. We can say that the comparison or simplified form of two quantities of the same kind is referred to as a ratio. This relation gives us how many times one quantity is equal to the other quantity. In simple words, the ratio is the number that can be used to express one quantity as a fraction of the other ones.
The two numbers in a ratio can only be compared when they have the same unit. We make use of ratios to compare two things. The sign used to denote a ratio is ‘:’.
A ratio can be written as a fraction, say 2/5. We happen to see various comparisons or say ratios in our daily life.
Hence, the ratio can be represented in three different forms, such as:
Key Points to Remember:
- The ratio should exist between the quantities of the same kind
- While comparing two things, the units should be similar
- There should be significant order of terms
- The comparison of two ratios can be performed, if the ratios are equivalent like the fractions
Definition of Proportion
Proportion is an equation that defines that the two given ratios are equivalent to each other. In other words, the proportion states the equality of the two fractions or the ratios. In proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other.
For example, the time taken by train to cover 100km per hour is equal to the time taken by it to cover the distance of 500km for 5 hours. Such as 100km/hr = 500km/5hrs.
Ratio and proportions are said to be faces of the same coin. When two ratios are equal in value, then they are said to be in proportion . In simple words, it compares two ratios. Proportions are denoted by the symbol ‘::’ or ‘=’.
The proportion can be classified into the following categories, such as:
Direct Proportion
Inverse proportion, continued proportion.
Now, let us discuss all these methods in brief:
The direct proportion describes the relationship between two quantities, in which the increases in one quantity, there is an increase in the other quantity also. Similarly, if one quantity decreases, the other quantity also decreases. Hence, if “a” and “b” are two quantities, then the direction proportion is written as a∝b.
The inverse proportion describes the relationship between two quantities in which an increase in one quantity leads to a decrease in the other quantity. Similarly, if there is a decrease in one quantity, there is an increase in the other quantity. Therefore, the inverse proportion of two quantities, say “a” and “b” is represented by a∝(1/b).
Consider two ratios to be a: b and c: d .
Then in order to find the continued proportion for the two given ratio terms, we convert the means to a single term/number. This would, in general, be the LCM of means.
For the given ratio, the LCM of b & c will be bc.
Thus, multiplying the first ratio by c and the second ratio by b, we have
First ratio- ca:bc
Second ratio- bc: bd
Thus, the continued proportion can be written in the form of ca: bc: bd
Ratio and Proportion Formula
Now, let us learn the Maths ratio and proportion formulas here.
Ratio Formula
Assume that, we have two quantities (or two numbers or two entities) and we have to find the ratio of these two, then the formula for ratio is defined as;
where a and b could be any two quantities .
Here, “a” is called the first term or antecedent , and “b” is called the second term or consequent .
Example: In ratio 4:9, is represented by 4/9, where 4 is antecedent and 9 is consequent.
If we multiply and divide each term of ratio by the same number (non-zero), it doesn’t affect the ratio.
Example: 4:9 = 8:18 = 12:27
Also, read: Ratio Formula
Proportion Formula
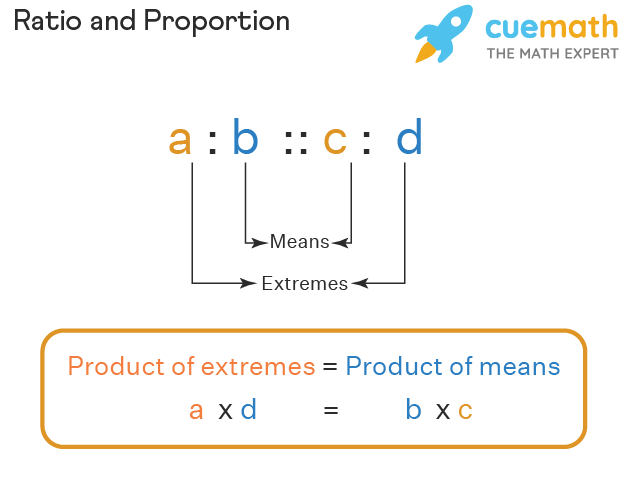
Now, let us assume that, in proportion, the two ratios are a:b & c:d. The two terms ‘b’ and ‘c’ are called ‘means or mean term,’ whereas the terms ‘a’ and ‘d’ are known as ‘ extremes or extreme terms.’
Example: Let us consider one more example of a number of students in a classroom. Our first ratio of the number of girls to boys is 3:5 and that of the other is 4:8, then the proportion can be written as:
3 : 5 :: 4 : 8 or 3/5 = 4/8
Here, 3 & 8 are the extremes, while 5 & 4 are the means.
Note: The ratio value does not affect when the same non-zero number is multiplied or divided on each term.
Important Properties of Proportion
The following are the important properties of proportion:
- Addendo – If a : b = c : d, then a + c : b + d
- Subtrahendo – If a : b = c : d, then a – c : b – d
- Dividendo – If a : b = c : d, then a – b : b = c – d : d
- Componendo – If a : b = c : d, then a + b : b = c+d : d
- Alternendo – If a : b = c : d, then a : c = b: d
- Invertendo – If a : b = c : d, then b : a = d : c
- Componendo and dividendo – If a : b = c : d, then a + b : a – b = c + d : c – d
Difference Between Ratio and Proportion
To understand the concept of ratio and proportion, go through the difference between ratio and proportion given here.
| S.No | Ratio | Proportion |
| 1 | The ratio is used to compare the size of two things with the same unit | The proportion is used to express the relation of two ratios |
| 2 | It is expressed using a colon (:), slash (/) | It is expressed using the double colon (::) or equal to the symbol (=) |
| 3 | It is an expression | It is an equation |
| 4 | Keyword to identify ratio in a problem is “to every” | Keyword to identify proportion in a problem is “out of” |
Fourth, Third and Mean Proportional
If a : b = c : d, then:
- d is called the fourth proportional to a, b, c.
- c is called the third proportion to a and b.
- Mean proportional between a and b is √(ab).
Comparison of Ratios
If (a:b)>(c:d) = (a/b>c/d)
The compounded ratio of the ratios: (a : b), (c : d), (e : f) is (ace : bdf).
Duplicate Ratios
If a:b is a ratio, then:
- a 2 :b 2 is a duplicate ratio
- √a:√b is the sub-duplicate ratio
- a 3 :b 3 is a triplicate ratio
Ratio and Proportion Tricks
Let us learn here some rules and tricks to solve problems based on ratio and proportion topics.
- If u/v = x/y, then uy = vx
- If u/v = x/y, then u/x = v/y
- If u/v = x/y, then v/u = y/x
- If u/v = x/y, then (u+v)/v = (x+y)/y
- If u/v = x/y, then (u-v)/v = (x-y)/y
- If u/v = x/y, then (u+v)/ (u-v) = (x+y)/(x-y), which is known as componendo -Dividendo Rule
- If a/(b+c) = b/(c+a) = c/(a+b) and a+b+ c ≠0, then a =b = c
Ratio and Proportion Summary
- Ratio defines the relationship between the quantities of two or more objects. It is used to compare the quantities of the same kind.
- If two or more ratios are equal, then it is said to be in proportion.
- The proportion can be represented in two different ways. Either it can be represented using an equal sign or by using a colon symbol. (i.e) a:b = c:d or a:b :: c:d
- If we multiply or divide each term of the ratio by the same number, it does not affect the ratio.
- For any three quantities, the quantities are said to be in continued proportion, if the ratio between the first and second quantity is equal to the ratio between the second and third quantity.
- For any four quantities, they are said to be in continued proportion, if the ratio between the first and second quantities is equal to the ratio between the third and fourth quantities
Ratio And Proportion Examples
Example 1:
Are the ratios 4:5 and 8:10 said to be in Proportion?
4:5= 4/5 = 0.8 and 8: 10= 8/10= 0.8
Since both the ratios are equal, they are said to be in proportion.
Are the two ratios 8:10 and 7:10 in proportion?
8:10= 8/10= 0.8 and 7:10= 7/10= 0.7
Since both the ratios are not equal, they are not in proportion.
Example 3:
Given ratio are-
Find a: b: c.
Multiplying the first ratio by 5, second by 3 and third by 6, we have
a:b = 10: 15
b:c = 15 : 6
c:d = 6 : 24
In the ratio’s above, all the mean terms are equal, thus
a:b:c:d = 10:15:6:24
Check whether the following statements are true or false.
a] 12 : 18 = 28 : 56
b] 25 people : 130 people = 15kg : 78kg
The given statement is false.
12 : 18 = 12 / 18 = 2 / 3 = 2 : 3
28 : 56 = 28 / 56 = 1 / 2 = 1 : 2
They are unequal.
b] 25 persons : 130 persons = 15kg : 78kg
The given statement is true.
25 people : 130 people = 5: 26
15kg : 78kg = 5: 26
They are equal.
The earnings of Rohan is 12000 rupees every month and Anish is 191520 per year. If the monthly expenses of every person are around 9960 rupees. Find the ratio of the savings.
Savings of Rohan per month = Rs (12000-9960) = Rs. 2040
Yearly income of Anish = Rs. 191520
Hence, the monthly income of Anish = Rs. 191520/12 = Rs. 15960.
So, the savings of Anish per month = Rs (15960 – 9960) = Rs. 6000
Thus, the ratio of savings of Rohan and Anish is Rs. 2040: Rs.6000 = 17: 50.
Twenty tons of iron is Rs. 600000 (six lakhs). What is the cost of 560 kilograms of iron?
1 ton = 1000 kg 20 tons = 20000 kg The cost of 20000 kg iron = Rs. 600000 The cost of 1 kg iron = Rs{600000}/ {20000} = Rs. 30 The cost of 560 kg iron = Rs 30 × 560 = Rs 16800
The dimensions of the rectangular field are given. The length and breadth of the rectangular field are 50 meters and 15 meters. What is the ratio of the length and breadth of the field?
Length of the rectangular field = 50 m
Breadth of the rectangular field = 15 m
Hence, the ratio of length to breadth = 50: 15
⇒ 50: 15 = 10: 3.
Thus, the ratio of length and breadth of the rectangular field is 10:3.
Obtain a ratio of 90 centimetres to 1.5 meters.
The given two quantities are not in the same units.
Convert them into the same units.
1.5 m = 1.5 × 100 = 150 cm
Hence, the required ratio is 90 cm: 150 cm
⇒ 90: 150 = 3: 5
Therefore, the ratio of 90 centimetres to 1.5 meters is 3: 5.
There exists 45 people in an office. Out of which female employees are 25 and the remaining are male employees. Find the ratio of
a] The count of females to males.
b] The count of males to females.
Count of females = 25
Total count of employees = 45
Count of males = 45 – 25 = 20
The ratio of the count of females to the count of males
The count of males to the count of females
Example 10:
Write two equivalent ratios of 6: 4.
Given Ratio : 6: 4, which is equal to 6/4.
Multiplying or dividing the same numbers on both numerator and denominator, we will get the equivalent ratio.
⇒(6×2)/(4×2) = 12/8 = 12: 8
⇒(6÷2)/(4÷2) = 3/2 = 3: 2
Therefore, the two equivalent ratios of 6: 4 are 3: 2 and 12: 8
Example 11 :
Out of the total students in a class, if the number of boys is 5 and the number of girls is 3, then find the ratio between girls and boys.
The ratio between girls and boys can be written as 3:5 (Girls: Boys). The ratio can also be written in the form of factor like 3/5.
Example 12:
Two numbers are in the ratio 2 : 3. If the sum of numbers is 60, find the numbers.
Given, 2/3 is the ratio of any two numbers.
Let the two numbers be 2x and 3x.
As per the given question, the sum of these two numbers = 60
So, 2x + 3x = 60
Hence, the two numbers are;
2x = 2 x 12 = 24
3x = 3 x 12 = 36
24 and 36 are the required numbers.
Maths ratio and proportion are used to solve many real-world problems. Register with BYJU’S – The Learning App and get solutions for many difficult questions in easy methodology and followed by the step-by-step procedure.
Frequently Asked Questions on Ratios and Proportion
What is the ratio give an example., what is a proportion give example, how to solve proportions with examples, what is the concept of ratios, what are the two different types of proportions.
The two different types of proportions are: Direct Proportion Inverse Proportion
Can we express ratio in terms of fractions?
Yes, we can express ratio in terms of fractions. For example, 3: 4 can be expressed as 3/4.
What is the formula for ratio and proportion?
The formula for ratio is: x:y ⇒ x/y, where x is the first term and y is the second term. The formula for proportion is: p: q :: r : s ⇒ p/q = r/s, Where p and r are the first term in the first and second ratio q and s are the second term and in the first and second ratio.
Find the means and extremes of the proportion 1: 2 :: 3: 4.
In the given proportion 1: 2 :: 3: 4, Means are 2 and 3 Extremes are 1 and 4.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment
Very helpful
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
WORD PROBLEMS ON RATIO AND PROPORTION
Problem 1 :
The average age of three boys is 25 years and their ages are in the proportion 3 : 5 : 7. Find the age of the youngest boy.
From the ratio 3 : 5 : 7, the ages of three boys are 3x, 5x and 7x.
Average age of three boys = 25
(3x + 5x + 7x)/3 = 25
Age of the first boy = 3x
Age of the first boy = 5x
Age of the first boy = 7x
So, the age of the youngest boy is 15 years.
Problem 2 :
John weighs 56.7 kilograms. If he is going to reduce his weight in the ratio 7 : 6, find his new weight.
Given : Original weight of John = 56.7 kg. He is going to reduce his weight in the ratio 7:6.
We can use the following hint to find his new weight, after it is reduced in the ratio 7 : 6.
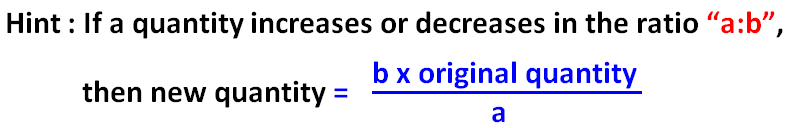
His new weight is
= (6 ⋅ 56.7)/7
So, John's new weight is 48.6 kg.
Problem 3 :
The ratio of the no. of boys to the no. of girls in a school of 720 students is 3 : 5. If 18 new girls are admitted in the school, find how many new boys may be admitted so that the ratio of the no. of boys to the no. of girls may change to 2 : 3.
Sum of the terms in the given ratio is
So, no. of boys in the school is
= 720 ⋅ (3/8)
= 270
No. of girls in the school is
= 720 ⋅ (5/8)
Given : Number of new girls admitted in the school is 18.
Let x be the no. of new boys admitted in the school.
After the above new admissions,
No. of boys in the school = 270 + x
No. of girls in the school = 450 + 18 = 468
Given : The ratio after the new admission is 2 : 3.
Then, we have
(270 + x) : 468 = 2 : 3
Use cross product rule.
3(270 + x) = 468 ⋅ 2
810 + 3x = 936
So, the number of new boys admitted in the school is 42.
Problem 4 :
The monthly incomes of two persons are in the ratio 4 : 5 and their monthly expenditures are in the ratio 7 : 9. If each saves $50 per month, find the monthly income of the second person.
From the given ratio of incomes ( 4 : 5 ),
Income of the 1st person = 4x
Income of the 2nd person = 5x
(Expenditure = Income - Savings)
Then, expenditure of the 1st person = 4x - 50
Expenditure of the 2nd person = 5x - 50
Expenditure ratio = 7 : 9 (given)
So, we have
(4x - 50) : (5x - 50) = 7 : 9
9(4x - 50) = 7(5x - 50)
36x - 450 = 35x - 350
Then, the income of the second person is
So, income of the second person is $500.
Problem 5 :
The ratio of the prices of two houses was 16 : 23. Two years later when the price of the first has increased by 10% and that of the second by $477, the ratio of the prices becomes 11 : 20. Find the original price of the first house.
From the given ratio 16 : 23,
Original price of the 1st house = 16x
Original price of the 2nd house = 23x
After increment in prices,
Price of the 1st house = 16x + 10% of 16x
= 16x + 1.6x
Price of the 2nd house = 23x + 477
After increment in prices, the ratio of prices becomes 11:20.
17.6x : (23x + 477) = 11 : 20
20(17.6x) = 11(23x + 477)
352x = 253x + 5247
Then, original price of the first house is
So, original price of the first house is $848.
Problem 6 :
Two numbers are respectively 20% and 50% are more than a third number, Find the ratio of the two numbers.
Let x be the third number.
Then, the first number is
= (100 + 20)% of x
= 120% of x
The second number is
= (100 + 50)% of x
= 150% of x
The ratio between the first number and second number is
= 1.2x : 1.5x
= 1.2 : 1.5
So, the ratio of two numbers is 4 : 5.
Problem 7 :
The milk and water in two vessels A and B are in the ratio 4:3 and 2:3 respectively. In what ratio, the liquids in both the vessels be mixed to obtain a new mixture in vessel C consisting half milk and half water ?
[4 : 3 ----> 4 + 3 = 7, M ----> 4/7, W ----> 3/7]
Let x be the quantity of mixture taken from vessel A to obtain a new mixture in vessel C.
Quantity of milk in x = (4/7)x = 4x/7
Quantity of water in x = (3/7)x = 3x/7
[2 : 3 ----> 2 + 3 = 5, M ---> 2/5, W ----> 3/5]
Let y be the quantity of mixture taken from vessel B to obtain a new mixture in vessel C.
Quantity of milk in y = (2/5)y = 2y/5
Quantity of water in y = (3/5)y = 3y/5
Vessel A and B :
Quantity of milk from A and B is
= 4x/7 + 2y/5
= (20x + 14y)/35
Quantity of water from A and B is
= (3x/7) + (3y/5)
= (15x + 21y)/35
According to the question, vessel C must consist half of the milk and half of the water.
That is, in vessel C, quantity of milk and water must be same.
There fore,
quantity of milk in (A + B) = quantity of water in (A + B)
(20x + 14y)/35 = (15x + 21y)/35
20x + 14y = 15x + 21y
x : y = 7 : 5
So, the required ratio is 7 : 5.
Problem 8 :
A vessel contains 20 liters of a mixture of milk and water in the ratio 3:2. From the vessel, 10 liters of the mixture is removed and replaced with an equal quantity of pure milk. Find the ratio of milk and water in the final mixture obtained.
[3 : 2 ----> 3 + 2 = 5, M ----> 3/5, W ----> 2/5]
In 20 liters of mixture,
no. of liters of milk = 20 ⋅ 3/5 = 12
no. of liters of water = 20 ⋅ 2/5 = 8
Now, 10 liters of mixture removed.
In this 10 liters of mixture, milk and water will be in the ratio 3 : 2.
no. of liters of milk in this 10 liters = 10 ⋅ 3/5 = 6
no. of liters of water in this 10 liters = 10 ⋅ 2/5 = 4
After removing 10 liters (1st time),
no. of liters of milk in the vessel = 12 - 6 = 6
no. of liters of water in the vessel = 8 - 4 = 4
Now, we add 10 liters of pure milk in the vessel,
After adding 10 liters of pure milk in the vessel,
no. of liters of milk in the vessel = 6 + 10 = 16
no. of liters of water in the vessel = 4 + 0 = 4
After removing 10 liters of mixture and adding 10 liters of pure milk, the ratio of milk and water is
So, the required ratio is 4 : 1.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Digital sat math problems and solutions (part - 43).
Sep 19, 24 11:30 AM
Best Way to Learn Mathematics
Sep 18, 24 11:29 AM
SAT Math Resources (Videos, Concepts, Worksheets and More)
Sep 16, 24 11:07 AM
Ratio and Proportion Word Problems — Examples & Practice - Expii

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

5.5: Ratios and Proportions
- Last updated
- Save as PDF
- Page ID 129556

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
After completing this section, you should be able to:
- Construct ratios to express comparison of two quantities.
- Use and apply proportional relationships to solve problems.
- Determine and apply a constant of proportionality.
- Use proportions to solve scaling problems.
Ratios and proportions are used in a wide variety of situations to make comparisons. For example, using the information from Figure 5.15, we can see that the number of Facebook users compared to the number of Twitter users is 2,006 M to 328 M. Note that the "M" stands for million, so 2,006 million is actually 2,006,000,000 and 328 million is 328,000,000. Similarly, the number of Qzone users compared to the number of Pinterest users is in a ratio of 632 million to 175 million. These types of comparisons are ratios.
Constructing Ratios to Express Comparison of Two Quantities
Note there are three different ways to write a ratio , which is a comparison of two numbers that can be written as: /**/(\$ 1 =0.82\,{€})/**/, how many dollars should you receive? Round to the nearest cent if necessary.
Example 5.31
Solving a proportion involving weights on different planets.
A person who weighs 170 pounds on Earth would weigh 64 pounds on Mars. How much would a typical racehorse (1,000 pounds) weigh on Mars? Round your answer to the nearest tenth.
Step 1: Set up the two ratios into a proportion. Notice the Earth weights are both in the numerator and the Mars weights are both in the denominator.
170 64 = 1,000 x 170 64 = 1,000 x
Step 2: Cross multiply, and then divide to solve.
170 x = 1,000 ( 64 ) 170 x = 64,000 170 x 170 = 64,000 170 x = 376.5 170 x = 1,000 ( 64 ) 170 x = 64,000 170 x 170 = 64,000 170 x = 376.5
So the 1,000-pound horse would weigh about 376.5 pounds on Mars.
Your Turn 5.31
Example 5.32, solving a proportion involving baking.
A cookie recipe needs /**/1{\text{ inch}} =/**/ how many miles). Then use that scale to determine the approximate lengths of the other borders of the state of Wyoming.
Example 5.38
Solving a scaling problem involving model cars.
Die-cast NASCAR model cars are said to be built on a scale of 1:24 when compared to the actual car. If a model car is 9 inches long, how long is a real NASCAR automobile? Write your answer in feet.
The scale tells us that 1 inch of the model car is equal to 24 inches (2 feet) on the real automobile. So set up the two ratios into a proportion. Notice that the model lengths are both in the numerator and the NASCAR automobile lengths are both in the denominator.
1 24 = 9 x 24 ( 9 ) = x 216 = x 1 24 = 9 x 24 ( 9 ) = x 216 = x
This amount (216) is in inches. To convert to feet, divide by 12, because there are 12 inches in a foot (this conversion from inches to feet is really another proportion!). The final answer is:
216 12 = 18 216 12 = 18
The NASCAR automobile is 18 feet long.
Your Turn 5.38
Check your understanding.
| /**/16:12/**/ | /**/12:16/**/ | /**/4:3/**/ |
| /**/16:12/**/ | /**/12:16/**/ | /**/16:28/**/ | /**/28:12/**/ | None of these |
| 625 | 6,250 | 3,456 | 345.6 | None of these |
Section 5.4 Exercises
| 1 | 2 | 3 | 4 | |
| 128 | 460 | /**/b/**/ | 541 | |
| $163.84 | /**/a/**/ | $277.76 | /**/c/**/ |

- Science Notes Posts
- Contact Science Notes
- Todd Helmenstine Biography
- Anne Helmenstine Biography
- Free Printable Periodic Tables (PDF and PNG)
- Periodic Table Wallpapers
- Interactive Periodic Table
- Periodic Table Posters
- Science Experiments for Kids
- How to Grow Crystals
- Chemistry Projects
- Fire and Flames Projects
- Holiday Science
- Chemistry Problems With Answers
- Physics Problems
- Unit Conversion Example Problems
- Chemistry Worksheets
- Biology Worksheets
- Periodic Table Worksheets
- Physical Science Worksheets
- Science Lab Worksheets
- My Amazon Books
Ratio and Proportion in Math

We use ratios and proportions when we compare numbers or quantities in math and in everyday life.
A ratio is a relationship between two numbers that compares one quantity to the other. Three ways of expressing ratios are using words, colons, or fractions: 2 to 3, 2:3, or 2/3. For example, if you have 2 apples and 3 oranges, the ratio of apples to oranges is 2:3.
A p roportion , on the other hand, is an equation stating that two ratios are equivalent. For example, if there are 2 apples for every 3 oranges in one basket, and 4 apples for every 6 oranges in another, the proportion is 2/3 = 4/6, meaning the ratio of apples to oranges is the same in both baskets.
In everyday life, we often use ratios and proportions without even realizing it. When following a recipe, you use ratios to measure ingredients. If you’re doubling a recipe, you’re using proportions to ensure that the increased amounts of ingredients keep the same ratio. When calculating miles per hour for a road trip, you use ratios to express your speed.
Ratio and Proportion Key Points
- A ratio is a relationship or comparison between two numbers or quantities.
- A proportion is an equation stating that two ratios are equal.
- Ratios are expressions, while proportions are equations.
- Ratios can be simplified just like fractions.
- Direct proportion: as one quantity increases, the other also increases at the same rate.
- Inverse proportion: as one quantity increases, the other decreases.
- Continued proportion: three quantities ‘a’, ‘b’, and ‘c’ are in continued proportion if a:b::b:c.
- In proportions, the product of extremes equals the product of means (a d = b c).
Now, let’s delve deeper into these two important mathematical concepts and explore their properties and applications.
A ratio expresses a relationship or comparison between any quantities. Generally they involve the natural numbers . In the realms of mathematics and science, a ratio finds various uses. For instance, when we talk about speed, it is a ‘rate’ – the ratio of distance covered in the time taken. Ratios are also fundamental in geometry, where they help to compare similar figures and trigonometry.
How to Simplify a Ratio
One crucial point is that you can simplify ratios. If you have a ratio of 10:15, it is the same as the simplified ratio 2:3. Here are simple steps for simplifying a ratio:
- Write the ratio a:b in the form of a fraction a/b. The top number of the fraction is its numerator, while the bottom number is the denominator. For example, if the ratio is 18:10, write 18:10.
- Find the greatest common factor of a and b. This is the largest number you can divide them by evenly. For 18 and 10, the greatest common factor is 2.
- Divide the numerator and denominator by the greatest common factor to get the simplified fraction. So, 18/10 becomes 9/5.
- Now, write the fraction is ratio form. 9/5 becomes 9:5.
Proportions
A proportion, as mentioned earlier, is an equation that equates two ratios. It serves as the foundation for numerous mathematical principles and real-world applications, from scaling models to converting units of measure.
Direct Proportion
In a direct proportion, two quantities increase or decrease together at the same rate. If “a” and “b” are two quantities, then the direct proportion is a∝b. If you travel at a constant speed, the distance you cover is directly proportional to the time you travel. This means that if you travel for 2 hours at 60 miles per hour, you cover 120 miles.
Inverse Proportion
In an inverse or indirect proportion, as one quantity increases, the other decreases. If “a” and “b” are two quantities, then the inverse proportion is a∝(1/b). For instance, the time taken to complete a task is inversely proportional to the number of people working on it. If 2 people can paint a house in 6 hours, 6 people can paint it in 2 hours, assuming all else stays the same.
Continued Proportions
In continued proportions, three quantities are in proportion. If ‘a’, ‘b’, and ‘c’ are in continued proportion, then a:b::b:c. This means that the ratio of ‘a’ to ‘b’ is the same as the ratio of ‘b’ to ‘c’. For example, 2, 6, and 18 are in continued proportion because 2/6 = 6/18.
Mathematical Properties of Proportions
Proportions have several unique mathematical properties.
The first term of a proportion is the antecedent. The second term is the consequent. For example, in the ratio 4:9, 4 is the antecedent and 9 is the consequent. If you multiply both the antecedent and consequent by the same non- zero number, the ratio remains unaffected.
The ‘extremes’ of a proportion are the first and last terms, while the ‘means’ are the second and third terms. In the proportion a/b = c/d, ‘a’ and ‘d’ are extremes, while ‘b’ and ‘c’ are means. For example, consider the proportion:
3 : 5 :: 4 : 8 or 3/5 = 4/8
Here, 3 and 8 are the extremes, while 5 and 4 are the means.
One key property is that the product of extremes equals the product of means (a d = b c). This property, known as the cross-multiplication rule , is a fundamental tool for solving proportions.
Here is a quick summary of the proportion properties:
- If a : b = c : d, then a + c : b + d
- If a : b = c : d, then a – c : b – d
- If a : b = c : d, then a – b : b = c – d : d
- If a : b = c : d, then a + b : b = c + d : d
- If a : b = c : d, then a : c = b: d If a : b = c : d, then b : a = d : c
- If a : b = c : d, then a + b : a – b = c + d : c – d
Additional Information
In higher mathematics, you encounter complex variations and applications of ratios and proportions, including compound ratios, duplicative and triplicate ratios, and the ratios of functions in calculus. The principles of ratios and proportions underpin the concept of scale in geometry, the basis of trigonometric identities, and much more.
Ratio and Proportion Worked Example Problems
- If 2 books cost $18, how much do 5 books cost?
Here, the ratio of books to cost is 2:18. If we increase the books to 5, we set up a proportion to find the cost: 2/18 = 5/x. Cross-multiplying gives 2x = 90, so x = $45.
- If 5 workers can complete a task in 7 hours, how long will it take 10 workers?
Here, the number of workers is inversely proportional to time. So, 57 = 10x. Solving for x gives x = 3.5 hours.
Understanding ratios and proportions is vital to navigating both academic mathematics and practical everyday situations. Their importance cannot be overstated, as these concepts form the building blocks for many areas of mathematics and real-world problem-solving.
- Ben-Chaim, David; Keret, Yaffa; Ilany, Bat-Sheva (2012). Ratio and Proportion: Research and Teaching in Mathematics Teachers. Springer Science & Business Media . ISBN 9789460917844.
- Burrell, Brian (1998). Merriam-Webster’s Guide to Everyday Math: A Home and Business Reference . Merriam-Webster. ISBN 9780877796213.
- Smith, D.E. (1925). History of Mathematics. Vol. 2. Ginn and Company.
- Van Dooren, Wim; De Bock, Dirk; Evers, Marleen; Verschaffel, Lieven (2009). “ Students’ Overuse of Proportionality on Missing-Value Problems: How Numbers May Change Solutions .” Journal for Research in Mathematics Education . 40 (2) 187–211.
Related Posts

Simplifying Ratios Pixel Picture ( Editable Word | PDF | Answers )
Simplifying Ratios Odd One Out ( Editable Word | PDF | Answers )
Equivalent Ratios Match-Up ( Editable Word | PDF | Answers )
Working with Ratio Practice Strips ( Editable Word | PDF | Answers )
Dividing in a Ratio Practice Strips ( Editable Word | PDF | Answers )
Dividing in a Ratio Fill in the Blanks ( Editable Word | PDF | Answers )
Dividing in a Ratio Crack the Code ( Editable Word | PDF | Answers )
Combining Ratios Practice Strips ( Editable Word | PDF | Answers )
Sharing and Combining Ratios Practice Strips ( Editable Word | PDF | Answers )
Solving Ratio Problems Practice Strips ( Editable Word | PDF | Answers )
Solving Ratio Problems Practice Grid ( Editable Word | PDF | Answers )
Harder Ratio Problems Practice Strips ( Editable Word | PDF | Answers )
Fractions and Ratio Worded Problems Practice Strips ( Editable Word | PDF | Answers )
Unitary Method Practice Strips ( Editable Word | PDF | Answers )
Unitary Method Match-Up ( Editable Word | PDF | Answers )
Best Buys Practice Strips ( Editable Word | PDF | Answers )
*NEW* Best Buys Fill in the Blanks ( Editable Word | PDF | Answers )
Currency Conversions Practice Strips ( Editable Word | PDF | Answers )
Proportion Worded Problems Practice Strips ( Editable Word | PDF | Answers )
Proportion Worded Problems Practice Grid ( Editable Word | PDF | Answers )
Mixed Ratio and Proportion Revision Practice Grid ( Editable Word | PDF | Answers )

Ratio: Problem Solving Textbook Exercise
Click here for questions, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Happiness Hub Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- Happiness Hub
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- Mathematics
How to Solve Proportions
Last Updated: July 6, 2024
This article was reviewed by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been viewed 105,747 times.

What is the "vertical" way to solve a proportion?

How can I solve a proportion with the "horizontal" method?

How do I solve a proportion step by step by cross-multiplying?

How do you find the missing value in a proportion with a table of ratios?

| 48 | 128 | |||
| x | 8 |
- Each column in this table represents a fraction. All of the fractions in this table are equal to each other.

| 48 | 64 | 128 | ||
| x | 4 | 8 |

| 32 | 48 | 64 | 128 | |
| 2 | x | 4 | 8 |

- The two answers are the same, which means your answer is correct.
How do you solve percent proportions?

How do you solve proportions algebraically?

- You can change the left hand side of the equation, as long as you do the same math to the right hand side.

- To get rid of the fraction on the left, multiply both sides by 27:

How do you solve a proportion with a variable on both sides?

- Warning : This is a difficult example. If you haven't learned about quadratic equations yet, you might want to skip this part.

- You can now solve this as a quadratic equation , using any method that you've learned.

Proportions Calculator, Practice Problems, and Answers

Community Q&A

- The algebraic method above works with any proportion. But for a specific proportion, there is often a faster way to use algebra to find the answer. As you learn more algebra, this will get easier. Thanks Helpful 0 Not Helpful 0

You Might Also Like

- ↑ https://www.youtube.com/watch?v=nwsDiID7UtQ
- ↑ https://www.youtube.com/watch?v=Uo8HgcyfRFI
- ↑ https://www.purplemath.com/modules/ratio2.htm
About This Article

To solve proportions, start by taking the numerator, or top number, of the fraction you know and multiplying it with the denominator, or bottom number, of the fraction you don’t know. Next, take that number and divide it by the denominator of the fraction you know. Now you can replace x with this final number. For example, to figure out “x” in the problem 3/4 = x/8, multiply 3 x 8 to get 24, then divide 24 / 4 to get 6, or the value of x. To learn how to use proportions to determine percentages, read on! Did this summary help you? Yes No
- Send fan mail to authors
Reader Success Stories
John Almacen
Nov 10, 2022
Did this article help you?

Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
Don’t miss out! Sign up for
wikiHow’s newsletter

Reading & Math for K-5
- Kindergarten
- Learning numbers
- Comparing numbers
- Place Value
- Roman numerals
- Subtraction
- Multiplication
- Order of operations
- Drills & practice
- Measurement
- Factoring & prime factors
- Proportions
- Shape & geometry
- Data & graphing
- Word problems
- Children's stories
- Leveled Stories
- Sentences & passages
- Context clues
- Cause & effect
- Compare & contrast
- Fact vs. fiction
- Fact vs. opinion
- Main idea & details
- Story elements
- Conclusions & inferences
- Sounds & phonics
- Words & vocabulary
- Reading comprehension
- Early writing
- Numbers & counting
- Simple math
- Social skills
- Other activities
- Dolch sight words
- Fry sight words
- Multiple meaning words
- Prefixes & suffixes
- Vocabulary cards
- Other parts of speech
- Punctuation
- Capitalization
- Narrative writing
- Opinion writing
- Informative writing
- Cursive alphabet
- Cursive letters
- Cursive letter joins
- Cursive words
- Cursive sentences
- Cursive passages
- Grammar & Writing
Breadcrumbs

Ratio word problems

Download & Print Only $7.90
Use ratios to solve these word problems
Students can use simple ratios to solve these word problems ; the arithmetic is kept simple so as to focus on the understanding of the use of ratios.

These worksheets are available to members only.
Join K5 to save time, skip ads and access more content. Learn More
What is K5?
K5 Learning offers free worksheets , flashcards and inexpensive workbooks for kids in kindergarten to grade 5. Become a member to access additional content and skip ads.
Our members helped us give away millions of worksheets last year.
We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.
Members skip ads and access exclusive features.
Learn about member benefits
This content is available to members only.
Ratio and Proportion
Ratio is used for comparing two quantities of the same kind. The ratio formula for two numbers, a and b is expressed as a : b or a/b. When two or more ratios are equal, they are said to be in proportion. The concept of ratio and proportion is based on fractions. Ratio and proportion are the key foundations for various other concepts in Mathematics. Ratio and proportion have their applications in solving many day-to-day problems, like when we compare heights, weights, distance or time or while adding ingredients in cooking, and so on.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. |
What is Ratio and Proportion?
A comparison of two quantities by division is called a ratio and the equality of two ratios is called proportion. A ratio can be written in different forms like x : y or x/y and is commonly read as, x is to y.
On the other hand, proportion is an equation that says that two ratios are equivalent. A proportion is written as x : y : : z : w, and is read as x is to y as z is to w. Here, x/y = z/w where w & y are not equal to 0.
Definition of Ratio
Ratio is the comparison of two quantities which is obtained by dividing the first quantity by the other. If a and b are two quantities of the same kind and with the same units, such that b is not equal to 0, then the quotient a/b is called the ratio between a and b. Ratios are expressed using the symbol of the colon (:). This means that ratio a/b has no unit and it can be written as a : b
Definition of Proportion
Proportion refers to the equality of two ratios. Two equivalent ratios are always in proportion. Proportions are denoted by the symbol (: :) and they help us to solve for unknown quantities. In other words, proportion is an equation or statement that is used to depict that the two ratios or fractions are equivalent. Four non-zero quantities, a, b, c, d are said to be in proportion if a : b = c : d. Now, let us consider the two ratios - 3 : 5 and 15 : 25. Here, 3 : 5 can be expressed as 3:5 = 3/5 = 0.6 and 15:25 can be expressed as 15:25 = 15/25 = 3/5 = 0.6. Since both the ratios are equal, we can say that these two are proportional.
There are two types of proportions.
Direct Proportion
Inverse proportion.
Direct proportion describes the direct relationship between two quantities. If one quantity increases, the other quantity also increases and vice-versa. Thus, a direct proportion is written as y ∝ x. For example, if the speed of a car is increased, then it covers more distance in a fixed period of time.
Inverse proportion describes the relationship between two quantities in which if one quantity increases, the other quantity decreases and vice-versa. Thus, an inverse proportion is written as y ∝ 1/x. For example, as the speed of a vehicle is increased, it will cover a fixed distance in less time.
Ratio and Proportion Formula
The formula for ratio is expressed as a : b ⇒ a/b, where,
- a = the first term or antecedent.
- b = the second term or consequent.
For example, ratio 2 : 7 is also represented as 2/7, where 2 is the antecedent and 7 is the consequent.
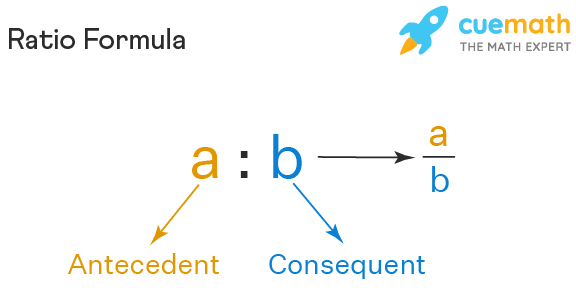
Now, in order to express a proportion for the two ratios, a : b and c : d, we write it as \(a: b:: c: d \longrightarrow \frac{a}{b}=\frac{c}{d}\)
- The two terms b and c are called mean terms.
- The two terms a and d are known as extreme terms.
- In a: b = c : d, the quantities a and b should be of the same kind with the same units, whereas, c and d may be separately of the same kind and of the same units. For example, 5 kg : 15 kg = Rs. 75 : Rs. 225
- The proportion formula can be expressed as, a/b = c/d or a : b : : c : d.
- In a proportion, the product of the means = the product of the extremes. Therefore, in the proportion formula a: b : : c : d, we get b × c = a × d. For example, in 5 : 15 :: 75 : 225, we will get 15 × 75 = 5 × 225
Difference Between Ratio and Proportion
The difference between ratio and proportion can be seen in the following table.
| Ratio | Proportion |
|---|---|
| It is used to compare the size of two quantities with the same unit. | It is used to express the relation of two ratios. |
| The symbols used to express a ratio - a colon (:), slash (/) | The symbol used to express a proportion - double colon (::) |
| It is referred to as an . | It is referred to as an . |
Important Notes on Ratio and Proportion
- Any two quantities with the same units can be compared.
- Two ratios are said to be in proportion only if they are equal.
- To check whether two ratios are equal and are in proportion, we can also use the cross-product method.
- If we multiply and divide each term of a ratio by the same number, the ratio remains the same.
- For any three quantities, if the ratio between the first and the second is equal to the ratio between the second and the third, then these are said to be in a continued proportion.
- Similarly, in the case of any four quantities in a continued proportion, the ratio between the first and the second is equal to the ratio between the third and the fourth.
- Ratio Analysis Formula
- Proportions Calculator
- Percent Proportion Calculator
- What does it mean for two ratios to be equivalent?
Examples on Ratio and Proportion
Example 1: Find out if the ratios 6:8 and 24:32 are in proportion.
The given ratios are 6:8 and 24:32. 6:8= 3/4 = 0.75 and 24:32 = 3/4= 0.75. Here, both the ratios are equal. Therefore, 6:8 and 24:32 are in proportion.
Example 2: There are 30 students in a class. The number of students who like Math and the ones who like Science is expressed in the ratio 2:3. Find the number of students who like Math and the ones who like Science.
Total number of students = 30. Let the number of students who like Math = 2x and the number of students who like Science = 3x. We can say that 2x + 3x = 30 ⇒ 5x = 30 ⇒ x = 6. Substituting the value of x = 6, we get the numbers of students who like Math = 2x = 2 × 6 = 12 and the number of students who like Science = 3x = 3 × 6 = 18.
Therefore, 12 students like Math and 18 students like Science.
Example 3: State true or false:
a.) Two ratios are said to be in proportion only if they are equivalent.
b.) In the ratio 6 : 8, 6 is the consequent and 8 is the antecedent.
a.) True, two ratios are said to be in proportion only if they are equivalent.
b.) False, in the ratio 6 : 8, 6 is the antecedent and 8 is the consequent.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Ratio and Proportion
Faqs on ratio and proportion.
Ratio is the comparison between the quantities with the same unit. It is obtained by dividing the first quantity by the other. If a and b are two quantities of the same kind and with the same units, such that b is not equal to 0, then the quotient a/b is called the ratio between a and b. On the other hand, proportion is defined to be a comparative relation between two ratios.
What is the Formula of Ratio and Proportion?
The ratio formula for any two quantities is expressed as a : b ⇒ a/b. On the other hand, the proportion formula is expressed as \(a : b : : c : d \longrightarrow \frac{a}{b}=\frac{c}{d}\).
What is the Difference Between Ratio and Proportion?
A ratio depicts a comparison between two quantities whereas proportion depicts the equality of two ratios.
How is Ratio and Proportion used in Real Life?
Ratio and proportion is used in our everyday lives. For example, the food that we eat has a fixed ratio of ingredients. The house or building that we stay in has a fixed ratio and proportion of cement and sand.
How is Ratio and Proportion Related to Each Other?
Ratio and proportion are related to each other. Ratio is used for comparing two quantities of the same kind. When two or more such ratios are equal, they are said to be in proportion.
How is Fraction Related to Ratio and Proportion?
A ratio can also be expressed as a fraction. For example, 1: 3 can also be written as 1/3. When a ratio is written in the fraction form, the fraction needs to be simplified. For example, when the fraction 13/39 is written in the form of a ratio, it will be 1:3. If it is an improper fraction, we do not convert it to a mixed fraction and leave it as an improper fraction because a ratio always compares two quantities.
What are the Two Parts of Proportion?
There are four parts in a proportion but based on their arrangement in the proportion, these are separated into two groups, the means, and the extremes. The outer terms are called extremes and the inner terms are called means. For example, in the proportion, 3 : 4 :: 24 : 32, the numbers 6 and 32 are extremes and 8 and 24 are means.
What is the Difference Between Direct and Inverse Proportion?
In direct proportion, the increase in one quantity leads to the increase in the other or vice versa whereas, in inverse proportion, the increase in one quantity leads to a decrease in the other.
A ratio compares values .
A ratio says how much of one thing there is compared to another thing.
Ratios can be shown in different ways:
| Use the ":" to separate the values: | 3 : 1 | |
| Or we can use the word "to": | 3 to 1 | |
| Or write it like a fraction: |
A ratio can be scaled up:
Try it Yourself
Using ratios.
The trick with ratios is to always multiply or divide the numbers by the same value .
| is the same as ×2 ×2 |
Example: A Recipe for pancakes uses 3 cups of flour and 2 cups of milk.
So the ratio of flour to milk is 3 : 2
To make pancakes for a LOT of people we might need 4 times the quantity, so we multiply the numbers by 4:
3 ×4 : 2 ×4 = 12 : 8
In other words, 12 cups of flour and 8 cups of milk .
The ratio is still the same, so the pancakes should be just as yummy.
"Part-to-Part" and "Part-to-Whole" Ratios
The examples so far have been "part-to-part" (comparing one part to another part).
But a ratio can also show a part compared to the whole lot .
Example: There are 5 pups, 2 are boys, and 3 are girls
Part-to-Part:
The ratio of boys to girls is 2:3 or 2 / 3
The ratio of girls to boys is 3:2 or 3 / 2
Part-to-Whole:
The ratio of boys to all pups is 2:5 or 2 / 5
The ratio of girls to all pups is 3:5 or 3 / 5
Try It Yourself
We can use ratios to scale drawings up or down (by multiplying or dividing).
| The height to width ratio of the Indian Flag is So for every (inches, meters, whatever) of height | |
| If we made the flag 20 inches high, it should be 30 inches wide. If we made the flag 40 cm high, it should be 60 cm wide (which is still in the ratio 2:3) | |
Example: To draw a horse at 1/10th normal size, multiply all sizes by 1/10th
This horse in real life is 1500 mm high and 2000 mm long, so the ratio of its height to length is
1500 : 2000
What is that ratio when we draw it at 1/10th normal size?
| 1500 : 2000 | = 1500 : 2000 | |
| = |
We can make any reduction/enlargement we want that way.
| Allie measured her foot and it was 21cm long, and then she measured her Mother's foot, and it was 24cm long. |
"I must have big feet, my foot is nearly as long as my Mom's!"
But then she thought to measure heights, and found she is 133cm tall, and her Mom is 152cm tall.
In a table this is:
| Allie | Mom | |
| Length of Foot: | 21cm | 24cm |
| Height: | 133cm | 152cm |
The "foot-to-height" ratio in fraction style is:
| Allie: | Mom: |
We can simplify those fractions like this:
And we get this (please check that the calcs are correct):
"Oh!" she said, "the Ratios are the same".
"So my foot is only as big as it should be for my height, and is not really too big."
You can practice your ratio skills by Making Some Chocolate Crispies
High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:
Dividing ratios
Here you will learn about dividing ratios, including how to share a quantity in a given ratio and real-life ratio problems.
Students will first learn about dividing ratios as part of ratios and proportional relationships in 6 th grade.
What is dividing ratios?
Dividing ratios is a way of sharing a quantity in given parts of a ratio. This can also be referred to as “dividing a quantity by a ratio.”
Problems involving dividing ratios can get quite wordy as they typically apply directly to real-life problems, usually involving money or food.
This means that it is likely that you will have to draw out the relevant information from the word problem. You can also expect your answers to be integers (whole numbers), decimals, fractions, or mixed numbers.
![problem solving ratio and proportion [FREE] Ratio Check for Understanding Quiz (Grade 6 to 7)](https://thirdspacelearning.com/wp-content/uploads/2023/07/Ratio-check-for-understanding-quiz-listing-image-.png)
[FREE] Ratio Check for Understanding Quiz (Grade 6 to 7)
Use this quiz to check your grade 6 to 7 students’ understanding of ratios. 10+ questions with answers covering a range of 6th and 7th grade ratio topics to identify areas of strength and support!
Share into a ratio
For example,
Share the amount \$ 10 in the ratio 2\text{:}3.
Here, the quantity is \$ 10, which is being shared in the parts of the ratio, 2 and 3. You need to find an equivalent ratio where the sum of the ratio parts is equal to 10.
Currently, you know the following facts:
The quantity =\$ 10
The ratio =2\text{:}3

You need to determine how many shares there are in the ratio overall.
You do this by adding the parts of the ratio together: 2+3=5 shares.
You have \$ 10 being split into 5 shares, and so you divide the quantity by the total amount of shares of the ratio 10\div5=2.
This is the value of one share .
So each share is worth \$ 2.

If there are 2 shares in the first part of the ratio, and each share is \$ 2, you multiply these values together to get the amount for that part of the ratio: 2 \times \$ 2=\$ 4.
Repeating this for the second part of the ratio, you get: 3 \times \$ 2=\$ 6.

The solution is \$ 4\text{:}\$ 6 (in that order).
To check your solution, add the final parts of the ratio together. If it is correct, the total should match the original quantity \$ 4+\$ 6=\$ 10. This is correct.
Note: Don’t be tempted to write your answer in its simplest form; you are finding an equivalent ratio where the parts total the quantity. That being said, it is a good way to check if your solution is correct. 4\text{:}6 does simplify to 2\text{:}3, the original ratio.
Bar modeling
The example above shows the use of bar modeling in how to share a quantity in a given ratio. Let’s have a look at another example using a three-part ratio.
A bag contains 24 sweets. Three friends share the sweets in a ratio of 1\text{:}2\text{:}3. How many sweets does each person get?
If person A gets 1 share, person B gets 2 shares and person C gets 3 shares, each time the parts are shared, you are using 1+2+3=6 parts.
Each share is therefore worth 24 \div 6=4.
If A gets 1 share, B gets 2 shares and C gets 3 shares, you have
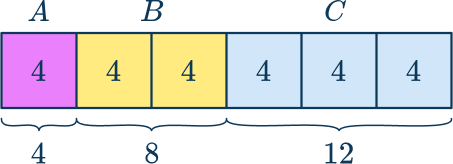
This gives us the ratio 4\text{:}8\text{:}12.
Common Core State Standards
How does this relate to 6 th grade math?
- Grade 6 – Ratios and Proportional Relationships (6.RP.A.3) Use ratio and rate reasoning to solve real-world and mathematical problems, example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
How to divide a quantity by a ratio
In order to divide a quantity by a ratio:
Add the parts of the ratio together.
Divide the quantity by the sum of the parts.
Multiply the share value by each part in the ratio.
Dividing ratios examples
Example 1: standard question.
Share the amount \$ 120 in the ratio 1\text{:}4.
2 Divide the quantity by the sum of the parts.
3 Multiply the share value by each part in the ratio.
Answer: \$ 24\text{:}\$ 96
Example 2: ratio sharing problem
A bag of sweets contains 600 sweets. The sweets were divided between boys and girls in the ratio 1\text{:}2. If there are 25 girls, how many sweets did each girl receive?
So you have the amount of 600 and the ratio 1\text{:}2.
200 \times 2=400
400 sweets were given to the 25 girls, so
400 \div 25=16
Answer: 16 sweets
Example 3: three part ratio
30 glue sticks were divided into 3 groups in the ratio 3\text{:}2\text{:}1. Calculate how many glue sticks each group received.
5 \times 2=10
5 \times 1=5
Answer: 15\text{:}10\text{:}5
Example 4: large quantities
A dealership sells hatchbacks and SUVs. 1,600 cars were sold in one year at the dealership in the ratio of 3\text{:}2 of hatchbacks to SUVs. How many hatchbacks were sold?
320 \times 2=640
Answer: 960 hatchbacks
Note: you do not need to work out all of the values in the new ratio but this can be helpful to check your answer is correct as the sum of these values must be the original amount.
Example 5: find one part
Concrete is made from 1 part cement, 2 parts sand, and 3 parts gravel. If Jarred wants to make 900 \, kg of concrete, how much sand does he need?
Answer: 300\mathrm{~kg} of sand
Example 6: recipe
A cocktail is made from mixing pineapple juice, orange juice, and sparkling water in the ratio 300\mathrm{~ml}\text{:}700\mathrm{~ml}\text{:}0.5\mathrm{~L}. How much of each quantity would be needed to make 6\mathrm{~L} of cocktail?
All the units must be the same in the ratio. 0.5\mathrm{~L}=500\mathrm{~ml} sparkling water, so the ratio of pineapple to orange to sparkling water is 300\text{:}700\text{:}500. This means the total is equal to
300+700+500=1500\mathrm{~ml}=1.5\mathrm{~L}
4\times{700}=2800\mathrm{~ml}
4\times{500}=2000\mathrm{~ml}
1,200\mathrm{~ml} of pineapple juice (=1.2\mathrm{~L})
2,800\mathrm{~ml} of orange juice (=2.8\mathrm{~L})
2,000\mathrm{~ml} of sparkling water (=2\mathrm{~L})
Example 7: bar modeling
The bar model below shows the ratio of the length of time the red, yellow, and green traffic lights are on during one sequence.

In one day, how many hours is each light on?
Adding up the number of shares in the bar, you have 3+2+5=10 .
A day has 24 hours, and so 24 \div 10=2.4 .
Each share represents 2.4 hours.
Looking at each color, you have
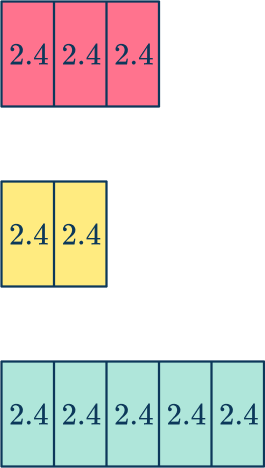
Red: 2.4 \times 3=7.2 hours
Yellow: 2.4 \times 2=4.8 hours
Green: 2.4 \times 5=12 hours
Red =7.2 hours ( 7 hours 12 minutes)
Yellow =4.8 hours ( 4 hours 48 minutes)
Green =12 hours
How to find the whole quantity given the amount of one part
In order to find the whole quantity given the amount of one part of the ratio:
Divide the amount by the correct part of the ratio.
Multiply the share value by the other parts in the ratio.
Add the amounts from each part of the ratio.
Example 8: being given one part of the ratio
Maxine and Niamh share some money in the ratio 3\text{:}5. Niamh receives \$ 45. How much money was shared?
You have been told that 5 parts are \$ 45. So you divide \$ 45 by 5 to find the value of each share.
45 \div 5=9
Each share represents \$ 9.
You can now work out Maxine’s part.
3 \times 9=\$ 27
Maxine has \$ 27 and Niamh has \$ 45 , so
\$ 27+\$ 45=\$ 72
Answer: \$ 72 was shared between Maxine and Niamh.
Here is the question as a bar model.
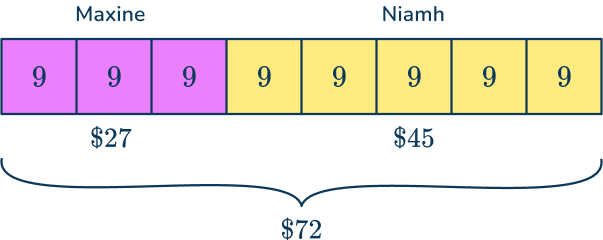
Teaching tips for dividing ratios
- Be sure that students understand the fundamentals of ratios before introducing dividing ratios. Step-by-step guide: Ratio Step-by-step guide: How to write a ratio
- Use word problems that relate to real life. For instance, if a recipe calls for a ratio of 2\text{:}3 (flour to sugar) and you need to divide this ratio for a smaller batch, show how to apply the division in context.
- If students are struggling, explain that dividing ratios relates to fractions because ratios can be expressed as fractions, and dividing a ratio is the same as dividing corresponding fractions. For example, dividing the ratio 4\text{:}5 by 2 is like dividing the fraction \cfrac{4}{5} by 2, which simplifies to \cfrac{2}{5}. As you can see, the first number of the ratio is the same as the numerator of the fraction, and the second number of the ratio is the denominator of the fraction. The quotient represents the new ratio after division.
- Solve several worksheet problems together as a class. Start with simple examples and gradually increase complexity.
Easy mistakes to make

- Dividing the ratio by each part As you need to divide something, it is incorrectly assumed that the amount is divided by each part of the ratio separately. Take for example “ divide \$ 120 in the ratio 2\text{:}3”. The answer is created by dividing \$ 120 by 2, and then \$ 120 by 3 to get \$ 60\text{:}\$ 40. This does not make sense as the answer ratio is not equivalent to the original ratio. Instead, the amount is divided by the sum of the parts in the ratio 120 \div(2+3)=120 \div 5=\$ 24, and then multiplied by each part in the ratio 24 \times 2=\$ 48,24 \times 3=\$ 72.
- Mixing units or using the wrong units Make sure that all the units in the ratio are the same. For example, in example 6, the answer shows the units in the ratio were in milliliters OR liters. You did not mix ml and L in the ratio.
- Not knowing what numbers to use Knowing what each number represents is very important for these types of questions. If you get confused, write the units down on each line of work.
- Counting the number of parts in the ratio, not the total number of shares The ratio 5\text{:}4 has 9 shares and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of work.
- Simplifying the answer When sharing a quantity in a given ratio, you are finding an equivalent ratio. You do not need to simplify the answer.
Related ratio lessons
- Ratio problem solving
- Simplifying ratios
- Unit rate math
- How to find the unit rate
- How to calculate exchange rates
- Ratio to fraction
- Ratio to percent
- Ratio scale
- Constant of proportionality
Practice dividing ratios questions
1. There are 10 boys and 9 girls. Each person is to receive the same amount of \$ 380. How much do all the boys, and all the girls receive? Express your answer as a ratio of boys\text{:}girls.

Amount: \$ 380
Ratio: 10\text{:}9
2. A company made a \$ 72,000 profit. It divides the profit between its employees (E) and its shareholders (S). The shareholders receive 55 \% of the profit. Calculate how much money the employees receive, giving your answer as a ratio in the form E\text{:}S.
Amount: \$ 72,000
Ratio: 45\text{:}55 \, (=9\text{:}11)
3. A swimming club is tracking its members. They have 7,668 members in the ratio of 2\text{:}3{:}4 \, (Males\text{:}Females\text{:}Children). Calculate how many members are children.
Amount: 7668
Ratio: 2\text{:}3\text{:}4
Answer: 3408 members are children
4. A farm is processing cherries into two categories, stalk attached or stalk not attached. In one season, the farm produces 150,000 cherries of which the ratio of those with and without stalks is 8\text{:}7 respectively. How many cherries are in each category? Express your answer as a ratio.
Amount: 150,000
Ratio: 8\text{:}7
5. Air is made up of nitrogen, oxygen, and other gasses in the ratio 78\text{:}21\text{:}1. A 5\mathrm{~L} balloon is filled with air. How much oxygen is in the balloon?
Amount: 5\mathrm{~L}=5000\mathrm{~ml}
Ratio: 78\text{:}21\text{:}1
The amount of oxygen is 1050\mathrm{~ml} or 1.05\mathrm{~L}.
6. A recipe for shortbread consists of plain flour, butter, and sugar in the ratio 3\text{:}2\text{:}1. Mary has 900 \, g of butter and plenty of sugar. How much plain flour does Mary need if she wants to use all of the butter?
Amount of butter: 900\mathrm{~g}
Part of the ratio for butter: 2
Part of the ratio for flour: 3
900\div{2}=450\mathrm{~g} ( 1 share)
450\times{3}=1350\mathrm{~g} (amount of flour)
Dividing ratios FAQs
Dividing ratios is a way of sharing a quantity in given parts of a ratio.
To divide a quantity by a ratio, first you add the parts of the ratio together, then divide the quantity by the sum of the parts, and finally, multiply the share value by each part in the ratio.
Dividing ratios is similar to dividing fractions because ratios can be expressed as fractions, and you divide the ratio by treating it like a fraction. For example, dividing the ratio 5\text{:}6 by 2 is like dividing the fraction \cfrac{5}{6} by 2.
Dividing ratios is useful in real-life situations such as resizing recipes, splitting expenses, or adjusting proportions in construction projects, as it helps maintain the correct balance between quantities.
The next lessons are
- Converting fractions decimals and percents
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (3rd to 8th Grade)
Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.
Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!
Privacy Overview
- Basic Math Formulas
- Trigonometry Formulas
- Integration Formulas
- Differentiation Formula
- Algebra Formulas
- Mensuration Formula
- Statistics Formulas
- Basic Geometry Formulas
- Sequences and Series Formulas
- Coordinate Geometry Formulas
- Trigonometric Table
- CBSE Class 8 Maths Formulas
- CBSE Class 9 Maths Formulas
- CBSE Class 10 Maths Formulas
- CBSE Class 11 Maths Formulas
Ratio and Proportion
Ratio and Proportion are used for comparison in mathematics. Ratio is a comparison of two quantities while Proportion is a comparison of two ratios.
Ratio and proportion are mostly about fractions. When you see a fraction written as a:b, that’s a ratio. A proportion is when two ratios are the same. In both cases, a and b are just any two whole numbers. Understanding ratios and proportions is really important. It helps you grasp many ideas in math and science. Let’s learn about Ratios and Proportions in detail, including their types, formulas, and examples.
Table of Content
Ratio and Proportion Definition
Ratio properties, ratio and proportion formula, difference between ratio and proportion, ratio and proportion examples.
When a fraction a/b is written a:b then it is termed as a ratio b. When two ratios let’s say a:b and c:d are equal a:b and c:d are said to be proportional to each other. Two proportional ratios are written as a:b::c:d.
Ratio Definition
Ratio is a comparison of two quantities of the same unit.
The ratio of two quantities is given by using the colon symbol (:). The ratio of two quantities a and b is given as
- a is called Antecedent
- b is called Consequent
The ratio a:b means ak/bk where k is the common factor. k is multiplied to give equivalent fractions whose simplest form will be a/b. We can read a:b as ‘a ratio b’ or ‘a to b’.
Key properties of Ratio are:
- If a ratio is multiplied by the same term both in antecedent and consequent then there is no change in the actual ratio. For example,
- If the antecedent and consequent of a ratio are divided by the same number then also there is no change in the actual ratio. For Example,
- If two ratios are equal then their reciprocals are also equal i.e. if a:b = c:d then b:a = d:c
- If two ratios are equal then their cross-multiplications are also equal. For Example
- The ratios for a pair of comparisons can be the same but the actual value may be different. For Example, 45:60 = 5:6 and 100:120 = 5:6 hence ratio 5:6 is same but actual value is different
Proportion Definition
Proportion refers to the comparison of ratios. If two ratios are equal then they are said to be proportionate to each other.
Two proportional ratios are represented by a double colon(::). If two ratios a:b and c:d are equal then they are represented as
a : b :: c : d
- a and d are called extreme terms
- b and c are called mean terms
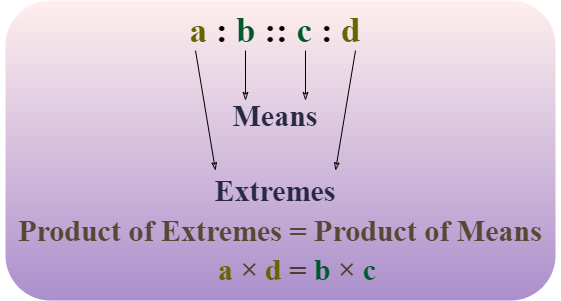
Proportion Properties
Key properties of Proportions are:
- For two ratios in proportion i.e. a/b = c/d, a/c = b/d holds true.
- For two ratios in proportion i.e. a/b = c/d, b/a = d/c holds true.
- For two ratios in proportion i.e. a:b::c:d, the product of mean terms is equal to the product of extreme terms i.e. ad = bc
- For two ratios in proportion i.e. a/b = c/d, (a + b)/b = (c + d)/d is true.
- For two ratios in proportion i.e. a/b = c/d, (a – b)/b = (c – d)/d is true.
Types of Proportions
There are three types of Proportions:
Direct Proportion
Inverse proportion, continued proportion.
Let’s learn about them in detail.
When two quantities increase and decrease in the same ratio then the two quantities are said to be in Direct Proportion. It means if one quantity increases then the other will also increase and if one will decrease then the other will also decrease.
It is represented as a ∝ b. For Example, Momentum is a product of mass and velocity hence, momentum is directly proportional to mass and velocity (p∝m or p∝v) which means if mass is constant and velocity is high then momentum will also be high and if velocity is constant then momentum will increase with an increase in mass.
When two quantities are inversely related to each other i.e. increase in one leads to a decrease in the other or a decrease in the other leads to an increase in the first quantity then the two quantities are said to be Inversely Proportional to each other.
For Example, Pressure is given by force divided by area (P = F/A). Here Pressure is inversely related to area which means a decrease in area will lead to an increase in pressure and an increase in area will lead to a decrease in pressure.
If the ratio a:b = b:c = c:d, then we see that the consequent of the first ratio is equal to the antecedent of the second ratio, and so on then the a:b:c:d is said to be in continued proportion.
- If the consequent and antecedent are not the same for two ratios then they can be converted into continued proportion by multiplying.
- For Example, in the case of a:b and c:d consequent and antecedent are not same then the continued proportion is given as ac:cb:bd.
- In the continued proportion a:b:c:d., c is called the third proportion, and d is called the fourth proportion.
Check : Ratio and Proportion
Let’s discuss the formulas on ratio and proportion in detail.
Ratio Formulas
The ratio of any two quantities a:b is given by a/b where a/b must be in simplest form. In case, you are not able to find the common factor between a and b then find the HCF or a and b and divide a and b with HCF to reduce it to the simplest form.
There are more formulas that we will discuss below:
Compound Ratios
When two ratios are multiplied then the new ratio is called the compound ratio. For example a:b and c:d are two ratios then ac:bd is a compound ratio.
Duplicate Ratios
For a:b, a 2 :b 2 is called duplicate ratios
For a:b, √a:√b is called sub-duplicate ratios
For a:b, a 3 :b 3 is called triplicate ratios
Proportion Formulas
These are the formulas used to solve problems of proportion:
- If a:b = c:d, then we can say that (a + c):(b + d), it is also called Addendo.
- If a:b = c:d, then we can say that (a – c):(b – d), it is also called Subtrahendo.
- If a:b = c:d, then we can say that (a – b):b = (c – d):d, it is also known as Dividendo.
- If a:b = c:d, then we can say that (a + b):b = (c + d):d, it is also known as Componendo.
- If a:b = c:d, then we can say that a:c = b:d, it is also known as Alternendo.
- If a:b = c:d, then we can say that b:a = d:c, it is also called Invertendo.
- If a:b = c:d, then we can say that (a + b):(a – b) = (c + d):(c – d), it is also known as Componendo and Dividendo.
- If a is proportional to b, then it means a = kb where k is a constant.
- If a is inversely proportional to b, then a = k/b, where k is a constant.
- Dividing or multiplying a ratio by a certain number gives an equivalent ratio.
Mean Proportion
Consider two ratios a:b = b:c then as per the rule of proportion product of the mean term is equal to the product of extremes, this means b 2 = ac, hence b = √ac is called mean proportion.
The comparison between Ratio and Proportion is tabulated below:
|
| |
|---|---|
| Ratio | Proportion |
| Ratio is used to compare two quantities of the same unit | Proportion is used to compare two ratios |
| Ratio is represented using (:), a/b = a:b | Proportion is represented using (::), a:b = c:d ⇒ a:b::c:d |
| Ratio is an expression | Proportion is an equation it equates two ratios |
Percentage Ratios and Percentages Fractions
Now let’s solve some questions on the properties of Ratio and Proportion we discussed so far.
Example 1. Is the ratio 5:10 proportional to 1:2?
5:10 divided by 5 gives 1:2. Thus, they are same to each other. So we can say that 5:10 is proportional to 1:2.
Example 2. Given a constant k, such that k:5 is proportional to 10:25. Find the value of k.
Since k:5 is proportional to 10:25 , we can write, k / 5 = 10 / 25 k = 10/25 × 5 = 2 So, the value of k is 2.
Example 3. Divide 100 into two parts such that they are proportional to 3:5.
Let’s the value of two parts are 3k and 5k, where k is a constant. Since the total sum of two parts is 100, we can write, 3k + 5k = 100 8k = 100 k = 12.5 So, the parts are 3k = 3 × 12.5 = 37.5 and 5k = 5 × 12.5 = 62.5
Example 4. If x 2 + 6y 2 = 5xy, then find the value of x/y.
Given, x 2 + 6y 2 = 5xy. Dividing the equation by y 2 , we get (x/y) 2 + 6 = 5 (x/y) Let’s x/y = t So, we can write, t 2 + 6 = 5t t 2 – 5t + 6 = 0 (t – 2)(t – 3) = 0 t = 2 or t = 3 Since, t = x/y, we get x/y = 2 or x/y = 3
Conclusion of Ratio and Proportion
Ratio and Proportion are fundamental concepts in mathematics that describe the relationship between quantities and their relative sizes. Ratios express the comparison between two quantities, while proportions establish equality between ratios. Understanding ratios and proportions is essential for solving problems involving scaling, mixing ingredients, financial analysis, and many other scenarios.
Ratios and Proportions – FAQs
What is definition of ratio.
Ratio is the comparison of two quantities of same units obtained by their division.
What is Definition of Proportion?
When two ratios are equivalent then the ratios are called to be in Proportion.
What is Direct Proportion?
When two quantities increase or decrease in the same ratio then the two quantities are said to be in direct proportion.
What is Continued Proportion?
When the consequent of the first ratio is the antecedent of the second ratio then two ratios are said to be in Proportion. For Example, a:b and b:c are in continued proportion and can be written as a:b:c.
What is Formula of Ratio and Proportion?
The Ratio of two quantities a and b is given by a:b = a/b and the formula for Proportion for two ratios a:b and c:d is a/b = c/d.
Can we Express Ratio In Terms of Fractions?
Yes, ratios can be expressed in terms of fractions. In fact, ratios are a specific type of fraction where two quantities are compared .
Please Login to comment...
Similar reads.
- Mathematics
- School Learning
- Math-Concepts
- Maths-Formulas
- Discord Launches End-To-End Encryption For Audio & Video Chats
- iPadOS 18 is Now Available: Complete Features and How to Install
- Microsoft’s Latest 365 Copilot Updates: Enhanced AI Tools for Excel, PowerPoint, and Teams
- Microsoft Unveils New AI Features: Copilot Pages and Autonomous AI Agents in Copilot Wave 2
- 10 Best PrimeWire Alternatives (2024)
Improve your Coding Skills with Practice
What kind of Experience do you want to share?

COMMENTS
Ratio problem solving is a collection of ratio and proportion word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem. ...
Ratio problem solving is a collection of word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem. A ratio is a relationship between two or more ...
How To Solve Proportion Word Problems? When solving proportion word problems remember to have like units in the numerator and denominator of each ratio in the proportion. Examples: Biologist tagged 900 rabbits in Bryer Lake National Park. At a later date, they found 6 tagged rabbits in a sample of 2000.
For example, ⅘ is a ratio and the proportion statement is 20/25 = ⅘. If we solve this proportional statement, we get: 20/25 = ⅘. 20 x 5 = 25 x 4. 100 = 100. Check: Ratio and Proportion PDF. Therefore, the ratio defines the relationship between two quantities such as a:b, where b is not equal to 0. Example: The ratio of 2 to 4 is ...
WORD PROBLEMS ON RATIO AND PROPORTION. Problem 1 : The average age of three boys is 25 years and their ages are in the proportion 3 : 5 : 7. Find the age of the youngest boy. Solution : From the ratio 3 : 5 : 7, the ages of three boys are 3x, 5x and 7x. Average age of three boys = 25. (3x + 5x + 7x)/3 = 25. 15x = 75.
The standard proportion problem is as follows: 5x=103 You are given two proportions and you want to solve for x. The best way to solve these types of equations is with cross multiplication. To cross multiply, you take the product of the numerator of the first ratio and the denominator of the second ratio.
Determine and apply a constant of proportionality. Use proportions to solve scaling problems. Ratios and proportions are used in a wide variety of situations to make comparisons. For example, using the information from Figure 5.15, we can see that the number of Facebook users compared to the number of Twitter users is 2,006 M to 328 M. Note ...
A ratio compares two numbers while a proportion equates two ratios. We use ratios and proportions when we compare numbers or quantities in math and in everyday life. A ratio is a relationship between two numbers that compares one quantity to the other. Three ways of expressing ratios are using words, colons, or fractions: 2 to 3, 2:3, or 2/3.
The Corbettmaths Practice Questions on Ratio. Previous: Percentages of an Amount (Non Calculator) Practice Questions
RATIO AND PROPORTION | Dr Austin Maths. Simplifying Ratios Pixel Picture (Editable Word | PDF | Answers ) Simplifying Ratios Odd One Out (Editable Word | PDF | Answers) Equivalent Ratios Match-Up (Editable Word | PDF | Answers) Working with Ratio Practice Strips (Editable Word | PDF | Answers) Dividing in a Ratio Practice Strips (Editable Word ...
Ratio & Proportion - 3 To solve problems, most people use either equivalent fractions or cross multiplying to solve proportions. Example If a turtle travels 5 inches every 10 seconds, how far will it travel in 50 seconds? What we are going to do is set up a proportion.
Proportion says that two ratios (or fractions) are equal. Example: We see that 1-out-of-3 is equal to 2-out-of-6. The ratios are the same, so they are in proportion. Example: Rope. A rope's length and weight are in proportion. When 20m of rope weighs 1kg, then: 40m of that rope weighs 2kg. 200m of that rope weighs 10kg.
Previous: Ratio: Difference Between Textbook Exercise Next: Reflections Textbook Exercise GCSE Revision Cards
Use ratio and rate reasoning to solve real-world and mathematical problems, for example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations. Grade 6 - Ratios and Proportions (6.RP.A.3b) Solve unit rate problems including those involving unit pricing and constant speed.
Find the product of these two numbers: 3. Divide by the last number in the proportion. Take the answer to your multiplication problem and divide it by the number you haven't used yet. (This is the green number in the example.) The result is the value of , the missing number in your proportion.
This math video tutorial provides a basic introduction into ratio and proportion word problems. Here is a list of examples and practice problems:Percentage ...
K5 Learning offers free worksheets, flashcards and inexpensive workbooks for kids in kindergarten to grade 5. Become a member to access additional content and skip ads. Ratio word problems. Students can use simple ratios to solve these word problems; the arithmetic is kept simple so as to focus on the understanding of the use of ratios.
Welcome to How to Solve Proportions with Mr. J! Need help with solving proportions? You're in the right place!Whether you're just starting out, or need a qui...
Math: Get ready courses; Get ready for 3rd grade; Get ready for 4th grade; Get ready for 5th grade; Get ready for 6th grade; Get ready for 7th grade; ... Equivalent ratio word problems; Equivalent ratios in the real world; Understand equivalent ratios in the real world; Ratios and rates: Quiz 2; Ratios on coordinate plane;
The concept of ratio and proportion is based on fractions. Ratio and proportion are the key foundations for various other concepts in Mathematics. Ratio and proportion have their applications in solving many day-to-day problems, like when we compare heights, weights, distance or time or while adding ingredients in cooking, and so on.
Using Ratios. The trick with ratios is to always multiply or divide the numbers by the same value. Example: A Recipe for pancakes uses 3 cups of flour and 2 cups of milk. So the ratio of flour to milk is 3 : 2. To make pancakes for a LOT of people we might need 4 times the quantity, so we multiply the numbers by 4: 3 ×4 : 2 ×4 = 12 : 8.
How does this relate to 6 th grade math? Grade 6 - Ratios and Proportional Relationships (6.RP.A.3) Use ratio and rate reasoning to solve real-world and mathematical problems, example, by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.
If a ratio is multiplied or divided by a certain number, the properties of the ratio do not change. For example, if we multiply 1: 2 by 5, we get 5: 10, which is the same as 1: 2; Also, check: Tricks To Solve Ratio and Proportion; Tips & Tricks To Solve Ratio & Proportion - Advance Level; Solved Questions on Ratios and Proportion Q 1.
The ratios for a pair of comparisons can be the same but the actual value may be different. For Example, 45:60 = 5:6 and 100:120 = 5:6 hence ratio 5:6 is same but actual value is different. Proportion refers to the comparison of ratios. If two ratios are equal then they are said to be proportionate to each other.
This resource is for students to practice writing and solving ratios in real-world problems. It can be used as an individual, partner, group, or a game practice activity after a lesson or throughout the school year. ... Full Collection KS3 Number KS3 Algebra KS3 Ratio and Proportion KS3 Geometry KS3 Probability KS3 Statistics GCSE Maths - Full ...