- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive

Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null & Alternative Hypotheses | Definitions, Templates & Examples
Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis ( H 0 ): There’s no effect in the population .
- Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:
- The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
- The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
Receive feedback on language, structure, and formatting
Professional editors proofread and edit your paper by focusing on:
- Academic style
- Vague sentences
- Style consistency
See an example

The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question.
- They both make claims about the population.
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
Prevent plagiarism. Run a free check.
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
General template sentences
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
- Alternative hypothesis ( H a ): Independent variable affects dependent variable.
Test-specific template sentences
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved August 5, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/
Is this article helpful?

Shaun Turney
Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Teach yourself statistics
Hypothesis Test for a Proportion
This lesson explains how to conduct a hypothesis test of a proportion, when the following conditions are met:
- The sampling method is simple random sampling .
- Each sample point can result in just two possible outcomes. We call one of these outcomes a success and the other, a failure.
- The sample includes at least 10 successes and 10 failures.
- The population size is at least 20 times as big as the sample size.
This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.
State the Hypotheses
Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.
Formulate an Analysis Plan
The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.
- Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
- Test method. Use the one-sample z-test to determine whether the hypothesized population proportion differs significantly from the observed sample proportion.
Analyze Sample Data
Using sample data, find the test statistic and its associated P-Value.
σ = sqrt[ P * ( 1 - P ) / n ]
z = (p - P) / σ
- P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a z-score, use the Normal Distribution Calculator to assess the probability associated with the z-score. (See sample problems at the end of this lesson for examples of how this is done.)
Interpret Results
If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.
Test Your Understanding
In this section, two hypothesis testing examples illustrate how to conduct a hypothesis test of a proportion. The first problem involves a a two-tailed test; the second problem, a one-tailed test.
Sample Size Calculator
As you probably noticed, the process of testing a hypothesis about a proportion can be complex. Stat Trek's Sample Size Calculator can do the same job quickly and easily. When you need to test a hypothesis, consider using the Sample Size Calculator. The calculator is free. It can found in the Stat Trek main menu under the Stat Tools tab. Or you can tap the button below.
Problem 1: Two-Tailed Test
The CEO of a large electric utility claims that 80 percent of his 1,000,000 customers are very satisfied with the service they receive. To test this claim, the local newspaper surveyed 100 customers, using simple random sampling. Among the sampled customers, 73 percent say they are very satisified. Based on these findings, can we reject the CEO's hypothesis that 80% of the customers are very satisfied? Use a 0.05 level of significance.
Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:
State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.
Null hypothesis: P = 0.80
Alternative hypothesis: P ≠ 0.80
- Formulate an analysis plan . For this analysis, the significance level is 0.05. The test method, shown in the next section, is a one-sample z-test .
σ = sqrt [(0.8 * 0.2) / 100]
σ = sqrt(0.0016) = 0.04
z = (p - P) / σ = (.73 - .80)/0.04 = -1.75
where P is the hypothesized value of population proportion in the null hypothesis, p is the sample proportion, and n is the sample size.
Since we have a two-tailed test , the P-value is the probability that the z-score is less than -1.75 or greater than 1.75. We use the Normal Distribution Calculator to find P(z < -1.75) = 0.04. Since the standard normal distribution is symmetric with a mean of zero, we know that P(z > 1.75) = 0.04. Thus, the P-value = 0.04 + 0.04 = 0.08.
- Interpret results . Since the P-value (0.08) is greater than the significance level (0.05), we cannot reject the null hypothesis.
Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the sample included at least 10 successes and 10 failures, and the population size was at least 10 times the sample size.
Problem 2: One-Tailed Test Suppose the previous example is stated a little bit differently. Suppose the CEO claims that at least 80 percent of the company's 1,000,000 customers are very satisfied. Again, 100 customers are surveyed using simple random sampling. The result: 73 percent are very satisfied. Based on these results, should we accept or reject the CEO's hypothesis? Assume a significance level of 0.05.
Null hypothesis: P >= 0.80
Alternative hypothesis: P < 0.80
σ = sqrt[ P * ( 1 - P ) / n ] = sqrt [(0.8 * 0.2) / 100]
- Interpret results . Since the P-value (0.04) is less than the significance level (0.05), we cannot accept the null hypothesis.
Have a thesis expert improve your writing
Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.
- Knowledge Base
- Null and Alternative Hypotheses | Definitions & Examples
Null and Alternative Hypotheses | Definitions & Examples
Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.
The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :
- Null hypothesis (H 0 ): There’s no effect in the population .
- Alternative hypothesis (H A ): There’s an effect in the population.
The effect is usually the effect of the independent variable on the dependent variable .
Table of contents
Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.
The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”
The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.
You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.
The null hypothesis is the claim that there’s no effect in the population.
If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.
Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.
Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).
Examples of null hypotheses
The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.
| ( ) | ||
| Does tooth flossing affect the number of cavities? | Tooth flossing has on the number of cavities. | test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ . |
| Does the amount of text highlighted in the textbook affect exam scores? | The amount of text highlighted in the textbook has on exam scores. | : There is no relationship between the amount of text highlighted and exam scores in the population; β = 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression.* | test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ . |
*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .
The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.
Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.
The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.
Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.
Examples of alternative hypotheses
The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.
| Does tooth flossing affect the number of cavities? | Tooth flossing has an on the number of cavities. | test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ . |
| Does the amount of text highlighted in a textbook affect exam scores? | The amount of text highlighted in the textbook has an on exam scores. | : There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0. |
| Does daily meditation decrease the incidence of depression? | Daily meditation the incidence of depression. | test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < . |
Null and alternative hypotheses are similar in some ways:
- They’re both answers to the research question
- They both make claims about the population
- They’re both evaluated by statistical tests.
However, there are important differences between the two types of hypotheses, summarized in the following table.
| A claim that there is in the population. | A claim that there is in the population. | |
|
| ||
| Equality symbol (=, ≥, or ≤) | Inequality symbol (≠, <, or >) | |
| Rejected | Supported | |
| Failed to reject | Not supported |
To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.
The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:
Does independent variable affect dependent variable ?
- Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
- Alternative hypothesis (H A ): Independent variable affects dependent variable .
Test-specific
Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.
| ( ) | ||
| test
with two groups | The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ . | The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ . |
| with three groups | The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ . | The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population. |
| There is no correlation between independent variable and dependent variable in the population; ρ = 0. | There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0. | |
| There is no relationship between independent variable and dependent variable in the population; β = 0. | There is a relationship between independent variable and dependent variable in the population; β ≠ 0. | |
| Two-proportions test | The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = . | The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ . |
Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.
The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).
The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).
A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).
A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 5 August 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/
Is this article helpful?

Shaun Turney
Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

8.8 Hypothesis Tests for a Population Proportion
Learning objectives.
- Conduct and interpret hypothesis tests for a population proportion.
Some notes about conducting a hypothesis test:
- The null hypothesis [latex]H_0[/latex] is always an “equal to.” The null hypothesis is the original claim about the population parameter.
- The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.” The form of the alternative hypothesis depends on the context of the question.
- If the alternative hypothesis is a “less than”, then the test is left-tail. The p -value is the area in the left-tail of the distribution.
- If the alternative hypothesis is a “greater than”, then the test is right-tail. The p -value is the area in the right-tail of the distribution.
- If the alternative hypothesis is a “not equal to”, then the test is two-tail. The p -value is the sum of the area in the two-tails of the distribution. Each tail represents exactly half of the p -value.
- Think about the meaning of the p -value. A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller p -value (for example, 0.001 as opposed to 0.04) even if using a significance level of 0.05. Similarly, for a large p -value such as 0.4, as opposed to a p -value of 0.056 (a significance level of 0.05 is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
- The significance level must be identified before collecting the sample data and conducting the test. Generally, the significance level will be included in the question. If no significance level is given, a common standard is to use a significance level of 5%.
Suppose the hypotheses for a hypothesis test are:
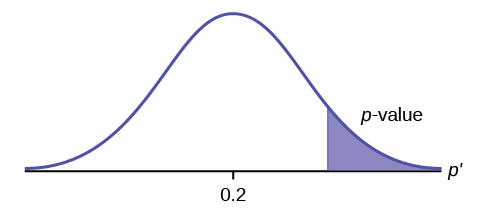
[latex]\begin{eqnarray*} H_0: & & p=20 \% \\ H_a: & & p \gt 20\% \end{eqnarray*}[/latex]
Because the alternative hypothesis is a [latex]\gt[/latex], this is a right-tail test. The p -value is the area in the right-tail of the distribution.
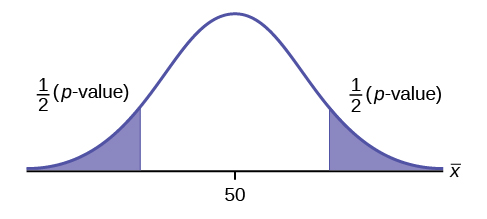
[latex]\begin{eqnarray*} H_0: & & p=50 \% \\ H_a: & & p \neq 50\% \end{eqnarray*}[/latex]
Because the alternative hypothesis is a [latex]\neq[/latex], this is a two-tail test. The p -value is the sum of the areas in the two tails of the distribution. Each tail contains exactly half of the p -value.
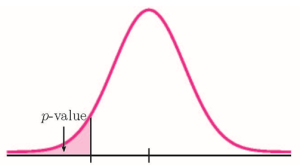
[latex]\begin{eqnarray*} H_0: & & p=10\% \\ H_a: & & p \lt 10\% \end{eqnarray*}[/latex]
Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tail test. The p -value is the area in the left-tail of the distribution.
Steps to Conduct a Hypothesis Test for a Population Proportion
- Write down the null and alternative hypotheses in terms of the population proportion [latex]p[/latex]. Include appropriate units with the values of the proportion.
- Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
- Collect the sample information for the test and identify the significance level.
- If [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution with [latex]\displaystyle{z=\frac{\hat{p}-p}{\sqrt{\frac{p \times (1-p)}{n}}}}[/latex].
- If one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use a binomial distribution.
- The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
- The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
- Write down a concluding sentence specific to the context of the question.
USING EXCEL TO CALCULE THE P -VALUE FOR A HYPOTHESIS TEST ON A POPULATION PROPORTION
The p -value for a hypothesis test on a population proportion is the area in the tail(s) of distribution of the sample proportion. If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution to find the p -value. If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use the binomial distribution to find the p -value.
If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex]:
- For x , enter the value for [latex]\hat{p}[/latex].
- For [latex]\mu[/latex] , enter the mean of the sample proportions [latex]p[/latex]. Note: Because the test is run assuming the null hypothesis is true, the value for [latex]p[/latex] is the claim from the null hypothesis.
- For [latex]\sigma[/latex] , enter the standard error of the proportions [latex]\displaystyle{\sqrt{\frac{p \times (1-p)}{n}}}[/latex].
- For the logic operator , enter true . Note: Because we are calculating the area under the curve, we always enter true for the logic operator.
- Use the appropriate technique with the norm.dist function to find the area in the left-tail or the area in the right-tail.
If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex]:
- The p -value is found using the binomial distribution.
- For x , enter the number of successes.
- For n , enter the sample size.
- For p , enter the the value of the population proportion [latex]p[/latex] from the null hypothesis.
- For the logic operator , enter true . Note: Because we are calculating an at most probability, the logic operator is always true.
- For p , enter the the value of the population proportion [latex]p[/latex] in the null hypothesis.
- For the logic operator , enter true . Note: Because we are calculating an at least probability, the logic operator is always true.
Marketers believe that 92% of adults own a cell phone. A cell phone manufacturer believes that number is actually lower. In a sample of 200 adults, 87% own a cell phone. At the 1% significance level, determine if the proportion of adults that own a cell phone is lower than the marketers’ claim.
Hypotheses:
[latex]\begin{eqnarray*} H_0: & & p=92\% \mbox{ of adults own a cell phone} \\ H_a: & & p \lt 92\% \mbox{ of adults own a cell phone} \end{eqnarray*}[/latex]
From the question, we have [latex]n=200[/latex], [latex]\hat{p}=0.87[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.92[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 200 \times 0.92=184 \geq 5 \\ n \times (1-p) & = & 200 \times (1-0.92)=16 \geq 5\end{eqnarray*}[/latex]
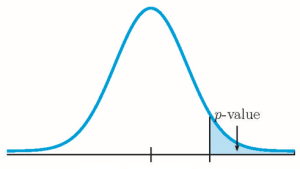
Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the area in the left tail of the distribution.
| norm.dist | ||
| 0.87 | 0.0046 | |
| 0.92 | ||
| sqrt(0.92*(1-0.92)/200) | ||
| true |
So the p -value[latex]=0.0046[/latex].
Conclusion:
Because p -value[latex]=0.0046 \lt 0.01=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 1% significance level there is enough evidence to suggest that the proportion of adults who own a cell phone is lower than 92%.
- The null hypothesis [latex]p=92\%[/latex] is the claim that 92% of adults own a cell phone.
- The alternative hypothesis [latex]p \lt 92\%[/latex] is the claim that less than 92% of adults own a cell phone.
- The function is norm.dist because we are finding the area in the left tail of a normal distribution.
- Field 1 is the value of [latex]\hat{p}[/latex].
- Field 2 is the value of [latex]p[/latex] from the null hypothesis. Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.92[/latex].
- Field 3 is the standard deviation for the sample proportions [latex]\displaystyle{\sqrt{\frac{p \times (1-p)}{n}}}[/latex].
- The p -value of 0.0046 tells us that under the assumption that 92% of adults own a cell phone (the null hypothesis), there is only a 0.46% chance that the proportion of adults who own a cell phone in a sample of 200 is 87% or less. This is a small probability, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the proportion of adults who own a cell phone is most likely less than 92%.
A consumer group claims that the proportion of households that have at least three cell phones is 30%. A cell phone company has reason to believe that the proportion of households with at least three cell phones is much higher. Before they start a big advertising campaign based on the proportion of households that have at least three cell phones, they want to test their claim. Their marketing people survey 150 households with the result that 54 of the households have at least three cell phones. At the 1% significance level, determine if the proportion of households that have at least three cell phones is less than 30%.
[latex]\begin{eqnarray*} H_0: & & p=30\% \mbox{ of household have at least 3 cell phones} \\ H_a: & & p \gt 30\% \mbox{ of household have at least 3 cell phones} \end{eqnarray*}[/latex]
From the question, we have [latex]n=150[/latex], [latex]\displaystyle{\hat{p}=\frac{54}{150}=0.36}[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.3[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 150 \times 0.3=45 \geq 5 \\ n \times (1-p) & = & 150 \times (1-0.3)=105 \geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right tail of the distribution.
| 1-norm.dist | ||
| 0.36 | 0.0544 | |
| 0.3 | ||
| sqrt(0.3*(1-0.3)/150) | ||
| true |
So the p -value[latex]=0.0544[/latex].
Because p -value[latex]=0.0544 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the 1% significance level there is not enough evidence to suggest that the proportion of households with at least three cell phones is more than 30%.
- The null hypothesis [latex]p=30\%[/latex] is the claim that 30% of households have at least three cell phones.
- The alternative hypothesis [latex]p \gt 30\%[/latex] is the claim that more than 30% of households have at least three cell phones.
- The function is 1-norm.dist because we are finding the area in the right tail of a normal distribution.
- Field 2 is the value of [latex]p[/latex] from the null hypothesis. Remember, we run the test assuming the null hypothesis is true, so that means we assume [latex]p=0.3[/latex].
- The p -value of 0.0544 tells us that under the assumption that 30% of households have at least three cell phones (the null hypothesis), there is a 5.44% chance that the proportion of households with at least three cell phones in a sample of 150 is 36% or more. Compared to the 1% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the claim that 30% of households have at least three cell phones is most likely correct.
A teacher believes that 70% of students in the class will want to go on a field trip to the local zoo. The students in the class believe the proportion is much higher and ask the teacher to verify her claim. The teacher samples 50 students and 39 reply that they would want to go to the zoo. At the 5% significance level, determine if the proportion of students who want to go on the field trip is higher than 70%.
[latex]\begin{eqnarray*} H_0: & & p = 70\% \mbox{ of students want to go on the field trip} \\ H_a: & & p \gt 70\% \mbox{ of students want to go on the field trip} \end{eqnarray*}[/latex]
From the question, we have [latex]n=50[/latex], [latex]\displaystyle{\hat{p}=\frac{39}{50}=0.78}[/latex], and [latex]\alpha=0.05[/latex].
[latex]\begin{eqnarray*} n \times p & = & 50 \times 0.7=35 \geq 5 \\ n \times (1-p) & = & 50 \times (1-0.7)=15 \geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right tail of the distribution.
| 1-norm.dist | ||
| 0.78 | 0.1085 | |
| 0.7 | ||
| sqrt(0.7*(1-0.7)/50) | ||
| true |
So the p -value[latex]=0.1085[/latex].
Because p -value[latex]=0.1085 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that the proportion of students who want to go on the field trip is higher than 70%.
- The null hypothesis [latex]p=70\%[/latex] is the claim that 70% of the students want to go on the field trip.
- The alternative hypothesis [latex]p \gt 70\%[/latex] is the claim that more than 70% of students want to go on the field trip.
- The p -value of 0.1085 tells us that under the assumption that 70% of students want to go on the field trip (the null hypothesis), there is a 10.85% chance that the proportion of students who want to go on the field trip in a sample of 50 students is 78% or more. Compared to the 5% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the teacher’s claim that 70% of students want to go on the field trip is most likely correct.
Joan believes that 50% of first-time brides in the United States are younger than their grooms. She performs a hypothesis test to determine if the percentage is the same or different from 50%. Joan samples 100 first-time brides and 56 reply that they are younger than their grooms. Use a 5% significance level.
[latex]\begin{eqnarray*} H_0: & & p=50\% \mbox{ of first-time brides are younger than the groom} \\ H_a: & & p \neq 50\% \mbox{ of first-time brides are younger than the groom} \end{eqnarray*}[/latex]
From the question, we have [latex]n=100[/latex], [latex]\displaystyle{\hat{p}=\frac{56}{100}=0.56}[/latex], and [latex]\alpha=0.05[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.5[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 100 \times 0.5=50 \geq 5 \\ n \times (1-p) & = & 100 \times (1-0.5)=50 \geq 5\end{eqnarray*}[/latex]
Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of area in the tails of the distribution.
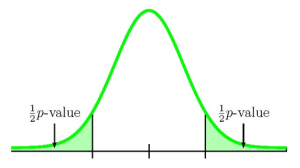
Because there is only one sample, we only have information relating to one of the two tails, either the left or the right. We need to know if the sample relates to the left or right tail because that will determine how we calculate out the area of that tail using the normal distribution. In this case, the sample proportion [latex]\hat{p}=0.56[/latex] is greater than the value of the population proportion in the null hypothesis [latex]p=0.5[/latex] ([latex]\hat{p}=0.56>0.5=p[/latex]), so the sample information relates to the right-tail of the normal distribution. This means that we will calculate out the area in the right tail using 1-norm.dist . However, this is a two-tailed test where the p -value is the sum of the area in the two tails and the area in the right-tail is only one half of the p -value. The area in the left tail equals the area in the right tail and the p -value is the sum of these two areas.
| 1-norm.dist | ||
| 0.56 | 0.1151 | |
| 0.5 | ||
| sqrt(0.5*(1-0.5)/100) | ||
| true |
So the area in the right tail is 0.1151 and [latex]\frac{1}{2}[/latex]( p -value)[latex]=0.1151[/latex]. This is also the area in the left tail, so
p -value[latex]=0.1151+0.1151=0.2302[/latex]
Because p -value[latex]=0.2302 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that the proportion of first-time brides that are younger than the groom is different from 50%.
- The null hypothesis [latex]p=50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is 50%.
- The alternative hypothesis [latex]p \neq 50\%[/latex] is the claim that the proportion of first-time brides that are younger than the groom is different from 50%.
- We use norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\mbox{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the left tail. The area in the right tail equals the area in the left tail, so we can find the p -value by adding the output from this function to itself.
- We use 1-norm.dist([latex]\hat{p}[/latex],[latex]p[/latex],[latex]\mbox{sqrt}(p*(1-p)/n)[/latex],true) to find the area in the right tail. The area in the left tail equals the area in the right tail, so we can find the p -value by adding the output from this function to itself.
- The p -value of 0.2302 is a large probability compared to the 5% significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the claim that the proportion of first-time brides who are younger than the groom is most likely correct.
Watch this video: Hypothesis Testing for Proportions: z -test by ExcelIsFun [7:27]
An online retailer believes that 93% of the visitors to its website will make a purchase. A researcher in the marketing department thinks the actual percent is lower than claimed. The researcher examines a sample of 50 visits to the website and finds that 45 of the visits resulted in a purchase. At the 1% significance level, determine if the proportion of visits to the website that result in a purchase is lower than claimed.
[latex]\begin{eqnarray*} H_0: & & p=93\% \mbox{ of visitors make a purchase} \\ H_a: & & p \lt 93\% \mbox{ of visitors make a purchase} \end{eqnarray*}[/latex]
From the question, we have [latex]n=50[/latex], [latex]x=45[/latex], and [latex]\alpha=0.01[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.93[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 50 \times 0.93=46.5 \geq 5 \\ n \times (1-p) & = & 50 \times (1-0.93)=3.5 \lt 5\end{eqnarray*}[/latex]
Because [latex]n \times (1-p) \lt 5[/latex] we use a binomial distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the probability of getting at most 45 successes in 50 trials.
| binom.dist | ||
| 45 | 0.2710 | |
| 50 | ||
| 0.93 | ||
| true |
So the p -value[latex]=0.2710[/latex].
Because p -value[latex]=0.2710 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the 1% significance level there is not enough evidence to suggest that the proportion of visitors who make a purchase is lower than 93%.
- The null hypothesis [latex]p=93\%[/latex] is the claim that 93% of visitors to the website make a purchase.
- The alternative hypothesis [latex]p \lt 93\%[/latex] is the claim that less than 93% of visitors to the website make a purchase.
- The function is binom.dist because we are finding the probability of at most 45 successes.
- Field 1 is the number of successes [latex]x[/latex].
- Field 2 is the sample size [latex]n[/latex].
- Field 3 is the probability of success [latex]p[/latex]. This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.93[/latex].
- The p -value of 0.2710 tells us that under the assumption that 93% of visitors make a purchase (the null hypothesis), there is a 27.10% chance that the number of visitors in a sample of 50 who make a purchase is 45 or less. This is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the proportion of visitors to the website who make a purchase adults is most likely 93%.
A drug company claims that only 4% of people who take their new drug experience any side effects from the drug. A researcher believes that the percent is higher than drug company’s claim. The researcher takes a sample of 80 people who take the drug and finds that 10% of the people in the sample experience side effects from the drug. At the 5% significance level, determine if the proportion of people who experience side effects from taking the drug is higher than claimed.
[latex]\begin{eqnarray*} H_0: & & p=4\% \mbox{ of people experience side effects} \\ H_a: & & p \gt 4\% \mbox{ of people experience side effects} \end{eqnarray*}[/latex]
From the question, we have [latex]n=80[/latex], [latex]\hat{p}=0.1[/latex], and [latex]\alpha=0.05[/latex].
To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.04[/latex]).
[latex]\begin{eqnarray*} n \times p & = & 80 \times 0.04=3.2 \lt 5\end{eqnarray*}[/latex]
Because [latex]n \times p \lt 5[/latex] we use a binomial distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the probability of getting at least 8 successes in 80 trials. (Note: In the sample of size 80, 10% have the characteristic of interest, so this means that [latex]80 \times 0.1=8[/latex] people in the sample have the characteristic of interest.)
| 1-binom.dist | ||
| 7 | 0.0147 | |
| 80 | ||
| 0.04 | ||
| true |
So the p -value[latex]=0.0147[/latex].
Because p -value[latex]=0.0147 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that the proportion of people who experience side effects from taking the drug is higher than 4%.
- The null hypothesis [latex]p=4\%[/latex] is the claim that 4% of the people experience side effects from taking the drug.
- The alternative hypothesis [latex]p \gt 4\%[/latex] is the claim that more than 4% of the people experience side effects from taking the drug.
- The function is 1-binom.dist because we are finding the probability of at least 8 successes.
- Field 1 is [latex]x-1[/latex] where [latex]x[/latex] is the number of successes. In this case, we are using the compliment rule to change the probability of at least 8 successes into 1 minus the probability of at most 7 successes.
- Field 3 is the probability of success [latex]p[/latex]. This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.04[/latex].
- The p -value of 0.0147 tells us that under the assumption that 4% of people experience side effects (the null hypothesis), there is a 1.47% chance that the number of people in a sample of 80 who experience side effects is 8 or more. This is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the proportion of people who experience side effects is most likely greater than 4%.
Concept Review
The hypothesis test for a population proportion is a well-established process:
- Find the p -value (the area in the corresponding tail) for the test using the appropriate distribution (normal or binomial).
- Compare the p -value to the significance level and state the outcome of the test.
Attribution
“ 9.6 Hypothesis Testing of a Single Mean and Single Proportion “ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.
Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
- Number Theory
- Data Structures
- Cornerstones
Hypothesis Testing Basics & One Sample Tests for Proportions
Introduction to hypothesis testing.
Hypothesis testing is a decision-making process by which we analyze a sample in an attempt to distinguish between results that can easily occur and results that are unlikely.
One begins with a claim or statement -- the reason for the study. For example, the claim might be "This coin in my pocket is fair."
Then we design a study to test the claim. In the case of the coin, we might decide to flip the coin 100 times.
Consider what could happen as a result of flipping that coin 100 times:
Suppose we saw that 99 out of 100 times, the flip resulted in "heads". Upon seeing this, no one in their right mind would still believe that the coin was fair. That notion would be completely rejected. A fair coin should come up "heads" roughly 50% of the time. The probability that a fair coin would come up "heads" 99 times out of 100 is so ridiculously small, that for all practical purposes we should never see it happen. The fact that we saw it happen constitutes significant statistical "evidence" that an assumption the coin is fair is very, very wrong.
If on the other hand, if one saw 54 out of 100 flips result in "heads", then -- while this doesn't exactly match our expectation that a fair coin should come up heads 50 out of 100 times -- it is not that far off the mark. It may be that we have a fair coin and the amount we are off is just due to the random nature of coin flips. It may also be that our coin is only slightly unfair -- perhaps coming up heads only 55% of the time. We simply don't know. We have no evidence either way. There is no reason for a person who previously believed the coin was fair, to change their mind. There is no significant statistical "evidence" that the coin is not fair.
These two circumstances capture the essence of all hypothesis testing...
We hold some belief of something before we start our experiment or study (e.g., the coin is fair). This belief might be based on our experience or history. It might be the more conservative thing to believe, given two possibilities. It might be categorized as a "no-change-has-happened" belief. Whatever it is -- if we see a highly unusual difference between what is expected under the assumption of that belief and what actually happens as a result of our sampling or experimentation, we consequently reject that belief. Seeing a more common outcome under the assumption of that belief, however, does not result in any rejection of that belief.
Attaching some statistical verbiage to these ideas, the "belief" described in the previous paragraph is called the null hypothesis , $H_0$. The alternative hypothesis , $H_1$, is what one will be forced to conclude is more likely the case after a rejection of the null hypothesis.
These hypotheses are typically stated in terms of values of population parameters, with the null hypothesis stating that the parameter in question "equals" some specific value, while the alternative hypothesis says this parameter is instead either not equal to, greater than, or less than that same specific value, depending on the context.
Importantly, the "claim" (the reason for the study) might sometimes be the null hypothesis, while other times it might be the alternative hypothesis. A common error among students learning statistics for the first time is to assume the claim is always just one of these.
Hypothesis Testing Using $p$-values
Returning to the example concerned with deciding whether a coin is fair or not based on flipping it 100 times, and assuming $p$ is the true proportion of heads that should be seen upon flipping the coin in our pocket, we first write the null and alternative hypotheses for our coin tossing experiment in the following way: $$H_0 : p = 0.50; \quad H_1 : p \neq 0.50$$
Recall that under the assumption of the null hypothesis, and as long as $np \ge 5$ and $nq \ge 5$, sample proportions $\widehat{p}$ should "pile up" in an approximately normal distribution with $$\mu = p = 0.5 \quad \textrm{ and } \quad \sigma = \sqrt{\frac{pq}{n}} = \sqrt{\frac{(0.5)(0.5)}{100}} = 0.05$$
Suppose as a result of our flipping the coin 100 times, we flipped heads $63$ times.
Then, the $z$-score for the corresponding sample proportion $\widehat{p} = 63/100 = 0.63$ is $$z_{0.63} = \frac{x - \mu}{\sigma} = \frac{0.63 - 0.5}{0.05} = 2.6$$ As a matter of verbiage -- for a hypothesis test involving a single proportion, the $z$-score associated with the sample proportion under consideration is called the test statistic . More generally, a test statistic indicates where on the related distribution the sample statistic falls.
Now we confront the question "Is what we saw unlikely enough that we should reject the null hypothesis? That is to say, does this particular observed $\widehat{p}$ happen so rarely when $p = 0.5$ that seeing it happen provides significant evidence that the $p \neq 0.5$?"
Towards this end, we consider the probability of seeing our test statistic, $z_{0.63} = 2.6$ -- or something even more extreme in the sense of the alternative hypothesis, in this standard normal distribution.
These "even more extreme" values (shaded red in the below diagram) certainly include those $z$ scores farther in the tail on the right (i.e., $z > 2.6$), but they also include those $z$-scores at a similar distance from the mean in the left tail of the distribution (i.e., $z < -2.6$). This is due to the fact that our alternative hypothesis simply says $p \neq 0.5$ -- it does not specify that $p$ is higher or lower than $0.5$. Had the alternative hypothesis been different, we might have limited ourselves to those $z$-scores in only one tail.

We can easily find $P_{\textrm{std norm}}(z 2.6)$ (i.e., the area shaded red above) with either a standard normal table, calculator, or a statistical programming environment like R.
As it turns out, $$P_{\textrm{std norm}}(z 2.6) \doteq 0.00932$$
Thus the probability, under the assumption that $p = 0.5$, that a sample will produce a $\widehat{p}$ as rare (or rarer) than what we saw in our one sample is only $0.00932$.
The probability just found is known as the p-value for the hypothesis test. More generally, the p-value is the probability of the observed outcome or an outcome at least that unusual (in the sense of the alternative hypothesis), under the assumption that the null hypothesis is true.
In this way, the p-value quantifies just how unusual what we saw actually was.
The question remains, however -- was the p-value we found small enough that we should conclude $p \neq 0.5$. (i.e., thus rejecting the null hypothesis)?
Understand that as long as the p-value is not zero, there is some possibility that $p = 0.50$ is actually true, and what we saw was just due to random chance. However, we want to make a decision -- one way or the other -- as to whether we believe this is a fair coin or not. We need to establish a cut-off probability, so that if the p-value is less than this cut-off, we consider the observed outcome unusual enough that it constitutes significant evidence that the null hypothesis should be rejected. This cut-off probability is called the significance level , and is denoted by $\alpha$.
As a standard, when a significance level is not specified at the outset, one typically uses $\alpha = 0.05$. Under this standard, observing something that happens less than 5% of the time is considered unusual enough to reject the null hypothesis.
Certainly, in this case we have $\textrm{p-value } \doteq 0.00932 < 0.05 = \alpha$ and the null hypothesis should be rejected. We indeed have statistically significant evidence that $p \neq 0.50$ and that the coin is consequently not a fair coin.
Hypothesis Testing Using Critical Values
Continuing with our the previous example, note that if all we care about is making a decision as to whether or not we believe the coin is fair, then we don't actually need the exact value of the p-value -- we just need to know if it is less than the significance level, $\alpha$.
With this in mind, recall that we know in a standard normal distribution, by the Empirical Rule, roughly 95% of the distribution falls between $z = -2$ and $z = 2$. A slightly better approximation puts this 95% in the region where $-1.96 \lt z \lt 1.96$. That leaves 5% of the distribution in the tails, where $z 1.96$ (i.e., the area outside the blue dashed lines below).

It should be patently obvious that if the test statistic (i.e., $z_{0.63} = 2.6$) falls in this region, the p-value (which agrees with the area of the red region above) must be smaller than 5%. Thus, we can immediately reject the null hypothesis, knowing $p \lt 0.05 = \alpha$.
The region of the distribution where it is unlikely for the test statistic to fall if the null hypothesis is indeed true (here, outside of $z = \pm1.96$) is called the rejection region , and the boundaries of the rejection region are known as critical values .
This (more traditional) way of performing a hypothesis test is certainly simpler to perform, especially in the absence of a calculator or software that can help with the calculation of the $p$-value. Although the lack of knowledge of the $p$-value makes comparing how significant results are relative to each other a bit more difficult.
Hypothesis Testing Using a Confidence Interval
There is one more way to perform a hypothesis test. It is only appropriate for two-tailed tests, but is simple to perform:
Simply find a confidence interval with confidence level of $(1-\alpha)$ where $\alpha$ is the significance level of the hypothesis test. Then, reject $H_0$ if the hypothesized population parameter (e.g., a proportion or mean) is not in the confidence interval.
This method of hypothesis testing can sometimes (very rarely) result in a different conclusion than the other two methods, as the confidence interval is built from an approximation of the standard deviation using the sample statistic ($\widehat{p}$, for example) as opposed to using the hypothesized population parameter (e.g. the proportion $p$ in the examples discussed here) to calculate the standard deviation.
Making an Inference
Regardless of whether you use $p$-values, critical values, or confidence intervals to conclude whether or not the null hypothesis should be rejected -- once this is done, it is time to make an inference -- that is to say, it is time to communicate what your conclusion says about the original claim.
When forming an inference, one should try to phrase it in a manner easily digested by someone that doesn't know a lot about statistics. In particular, one should not use words like "null hypothesis", "p-value", "significance level", etc.
If the claim is the null hypothesis, you can start your inference with " There is enough evidence to reject the claim that... " if you rejected the null hypothesis, and with " There is not enough evidence to reject the claim that... " if you failed to reject the null hypothesis.
If the claim is the alternative hypothesis, you can instead start your inference with " There is enough evidence to support the claim that... " if you rejected the null hypothesis, and with " There is not enough evidence to support the claim that... " if you failed to reject the null hypothesis.
Alternatively, you can use phrases like " significantly different ", " significantly higher ", or " significantly lower " in the statement of your inference.
Very importantly -- one should never use the word "prove" in an inference. No matter the result of the hypothesis test, there is always a possibility of error. For example, at a significance level of $0.05$, one should absolutely expect that one in twenty experiments/observations will produce a p-value less than that $0.05$, which could then be erroneously deemed "statistically significant evidence" -- a point humorously driven home by this xkcd.com comic strip .
Indeed, there are two types of errors we could make when conducting a hypothesis test. We could -- as just described -- mistakenly reject a true null hypothesis (known as a Type I error ), or we could also fail to reject a false hypothesis (known as a Type II error ). Sadly, these firmly entrenched names for the types of errors one might commit are not very descriptive and consequently can easily be confused with each another. As a useful way to keep them straight, one might remember Aesop's fable of The Boy Who Cried Wolf" . In part I of this story, the villagers commit a Type I error by reacting to the presence of a wolf when there is none. In part II of this story, the villagers commit a Type II error by failing to react when there actually is a wolf.
The probability of a Type I error is, of course, the significance level for the test, $\alpha$. The probability of a Type II error is denoted by $\beta$, and is impossible to calculate without actually knowing the actual value of the population parameter in question.
As one last bit of verbiage, the probability of rejecting a false null hypothesis is consequently $1 - \beta$, and is known as the power of the test . We can increase the power of a test by either increasing the sample size $n$, or the significance level, $\alpha$.
Chapter 8: Inference for One Proportion
Hypothesis test for a population proportion (3 of 3), learning objectives.
- Conduct a hypothesis test for a population proportion. State a conclusion in context.
- Interpret the P-value as a conditional probability in the context of a hypothesis test about a population proportion.
- Distinguish statistical significance from practical importance.
- From a description of a study, evaluate whether the conclusion of a hypothesis test is reasonable.
More about the P-Value
The P-value is a probability that describes the likelihood of the data if the null hypothesis is true. More specifically, the P-value is the probability that sample results are as extreme as or more extreme than the data if the null hypothesis is true. The phrase “as extreme as or more extreme than” means farther from the center of the sampling distribution in the direction of the alternative hypothesis.
More generally, we view the P-value a description of the strength of the evidence against the null hypothesis and in support of the alternative hypothesis. But the P-value is a probability about sample results, not about the null or alternative hypothesis.
One More Note about P-Values and the Significance Level
You may wonder why 5% is often selected as the significance level in hypothesis testing and why 1% is also a commonly used level. It is largely due to just convenience and tradition. When Ronald Fisher (one of the founders of modern statistics) published one of his tables, he used a mathematically convenient scale that included 5% and 1%. Later, these same 5% and 1% levels were used by other people, in part just because Fisher was so highly esteemed. But mostly, these are arbitrary levels.
The idea of selecting some sort of relatively small cutoff was historically important in the development of statistics. But it’s important to remember that there is really a continuous range of increasing confidence toward the alternative hypothesis, not a single all-or-nothing value. There isn’t much meaningful difference, for instance, between the P-values 0.049 and 0.051, and it would be foolish to declare one case definitely a “real” effect and the other case definitely a “random” effect. In either case, the study results are roughly 5% likely by chance if there’s no actual effect.
Whether such a P-value is sufficient for us to reject a particular null hypothesis ultimately depends on the risk of making the wrong decision and the extent to which the hypothesized effect might contradict our prior experience or previous studies.
Sample Size and Hypothesis Testing
Consider our earlier example about teenagers and Internet access. According to the Kaiser Family Foundation, 84% of U.S. children ages 8 to 18 had Internet access at home as of August 2009. Researchers wonder if this number has changed since then. The hypotheses we tested were:
- H 0 : p = 0.84
- H a : p ≠ 0.84
The original sample consisted of 500 children, and 86% of them had Internet access at home. The P-value was about 0.22, which was not strong enough to reject the null hypothesis. There was not enough evidence to show that the proportion of all U.S. children ages 8 to 18 have Internet access at home.
Suppose we sampled 2,000 children and the sample proportion was still 86%. Our test statistic would be Z ≈ 2.44, and our P-value would be about 0.015. The larger sample size would allow us to reject the null hypothesis even though the sample proportion was the same.

Why does this happen? Larger samples vary less, so a sample proportion of 0.86 is more unusual with larger samples than with smaller samples if the population proportion is really 0.84. This means that if the alternative hypothesis is true, a larger sample size will make it more likely that we reject the null. Therefore, we generally prefer a larger sample as we have seen previously.
Drawing Conclusions from Hypothesis Tests
It is tempting to get involved in the details of a hypothesis test without thinking about how the data was collected. Whether we are calculating a confidence interval or performing a hypothesis test, the results are meaningless without a properly designed study. Consider the following exercises about how data collection can affect the results of a study.
Learn By Doing
Let’s summarize.
In this section, we looked at the four steps of a hypothesis test as they relate to a claim about a population proportion.
Step 1: Determine the hypotheses.
- The hypotheses are claims about the population proportion, p .
- The null hypothesis is a hypothesis that the proportion equals a specific value, p 0 .
- The alternative hypothesis is the competing claim that the parameter is less than, greater than, or not equal to p 0 .
Step 2: Collect the data.
Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the sample proportion can be np ≥ 10 and n (1 − p ) ≥ 10.
Step 3: Assess the evidence.
- Determine the test statistic which is the z -score for the sample proportion. The formula is: [latex]Z=\frac{\stackrel{ˆ}{p}-{p}_{0}}{\sqrt{\frac{{p}_{0}(1-{p}_{0})}{n}}}[/latex]
- Use the test statistic, together with the alternative hypothesis to determine the P-value. You can use a standard normal table (or Z -table) or technology (such as the simulations on the second page of this topic) to find the P-value.
- If the alternative hypothesis is greater than, the P-value is the area to the right of the test statistic. If the alternative hypothesis is less than, the P-value is the area to the left of the test statistic. If the alternative hypothesis is not equal to, the P-value is equal to double the tail area beyond the test statistic.
Step 4: Give the conclusion.
- A small P-value says the data is unlikely to occur if the null is true. If the P-value is less than or equal to the significance level, we reject the null hypothesis and accept the alternative hypothesis instead.
- If the P-value is greater than the significance level, we say we “fail to reject” the null hypothesis. We never say that we “accept” the null hypothesis. We just say that we don’t have enough evidence to reject it. This is equivalent to saying we don’t have enough evidence to support the alternative hypothesis.
- We write the conclusion in the context of the research question. Our conclusion is usually a statement about the alternative hypothesis (we accept H a or fail to accept H a ) and should include the P-value.
Other Hypothesis Testing Notes
Remember that the P-value is the probability of seeing a sample proportion as extreme as the one observed from the data if the null hypothesis is true. The probability is about the random sample, not about the null or alternative hypothesis.
A larger sample size makes it more likely that we will reject the null hypothesis if the alternative is true. Another way of thinking about this is that increasing the sample size will decrease the likelihood of a type II error. Recall that a type II error is failing to reject the null hypothesis when the alternative is true.
Increasing the sample size can have the unintended effect of making the test sensitive to differences so small they don’t matter. A statistically significant difference is one large enough that it is unlikely to be due to sampling variability alone. Even a difference so small that it is not important can be statistically significant if the sample size is big enough.
Finally, remember the phrase “garbage in, garbage out.” If the data collection methods are poor, then the results of a hypothesis test are meaningless. No statistical methods can create useful information if our data comes from convenience or voluntary response samples. Additionally, the results of a hypothesis test apply only to the population from whom the sample was chosen.
- Concepts in Statistics. Provided by : Open Learning Initiative. Located at : http://oli.cmu.edu . License : CC BY: Attribution

Privacy Policy
Article Categories
Book categories, collections.
- Academics & The Arts Articles
- Math Articles
- Statistics Articles
How to Test a Null Hypothesis Based on One Population Proportion
Statistics for dummies.

Sign up for the Dummies Beta Program to try Dummies' newest way to learn.
You can use a hypothesis test to test a statistical claim about a population proportion when the variable is categorical (for example, gender or support/oppose) and only one population or group is being studied (for example, all registered voters).
The test looks at the proportion ( p ) of individuals in the population who have a certain characteristic — for example, the proportion of people who carry cellphones. The null hypothesis is H 0 : p = p 0 , where p 0 is a certain claimed value of the population proportion, p . For example, if the claim is that 70% of people carry cellphones, p 0 is 0.70. The alternative hypothesis is one of the following:
The formula for the test statistic for a single proportion (under certain conditions) is:

and z is a value on the Z -distribution. To calculate the test statistic, do the following:
Calculate the sample proportion,
by taking the number of people in the sample who have the characteristic of interest (for example, the number of people in the sample carrying cellphones) and dividing that by n, the sample size.
where p o is the value in H o .
Calculate the standard error,
Divide your result from Step 2 by your result from Step 3.
To interpret the test statistic, look up your test statistic on the standard normal ( Z- ) distribution and calculate the p- value.
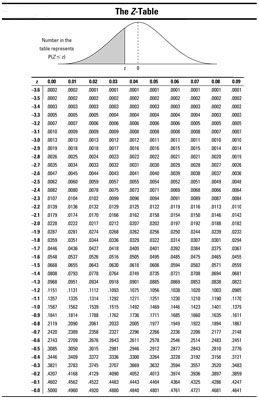
The conditions for using this test statistic are that
For example, suppose Cavifree claims that four out of five dentists recommend Cavifree toothpaste to their patients. In this case, the population is all dentists, and p is the proportion of all dentists who recommended Cavifree. The claim is that p is equal to “four out of five,” or p 0 is 4 divided by 5 = 0.80. You suspect that the proportion is actually less than 0.80. Your hypotheses are H 0 : p = 0.80 versus H a : p < 0.80.
Suppose that 151 out of your sample of 200 dental patients reported receiving a recommendation for Cavifree from their dentist. To find the test statistic for these results, follow these steps:
and n = 200.
Because p o = 0.80, take p(hat)-p 0 =0.755 – 0.80 = –0.045 as the numerator of the test statistic.
Next, the standard error equals
(the denominator of the test statistic).
The test statistic is
Because the resulting test statistic is negative, it means your sample results are –1.61 standard errors below (less than) the claimed value for the population. How often would you expect to get results like this if H 0 were true? The chance of being at or beyond (in this case less than) –1.61 is 0.0537. (Keep the negative with the number and look up –1.61 in the above Z -table.) This result is your p- value because H a is a less-than hypothesis.
Because the p- value is greater than 0.05 (albeit not by much), you don’t have quite enough evidence for rejecting H 0 . You conclude that the claim that 80% of dentists recommend Cavifree can’t be rejected, according to your data. However, it’s important to report the actual p -value too, so others can make their own decisions.
You might ask, “Hey, the sample proportion of 0.755 is way lower than the claimed proportion of 0.80. Why did the hypothesis test reject H 0 since 0.755 is less than 0.80?” Because in this case, 0.755 is not significantly less than 0.80. You also need to factor in variation using the standard error and the normal distribution to be able to say something about the entire population of dentists.
The letter p is used two different ways in this example: p -value and p . The letter p by itself indicates the population proportion, not the p -value. Don’t get confused. Whenever you report a p -value, be sure you add –value so it’s not confused with p, the population proportion .
About This Article
This article is from the book:.
- Statistics For Dummies ,
About the book author:
Deborah J. Rumsey , PhD, is an Auxiliary Professor and Statistics Education Specialist at The Ohio State University. She is the author of Statistics For Dummies, Statistics II For Dummies, Statistics Workbook For Dummies, and Probability For Dummies.
This article can be found in the category:
- Statistics ,
- Statistics For Dummies Cheat Sheet
- Checking Out Statistical Confidence Interval Critical Values
- Handling Statistical Hypothesis Tests
- Statistically Figuring Sample Size
- Surveying Statistical Confidence Intervals
- View All Articles From Book
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
10.1 - setting the hypotheses: examples.
A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or differences between means or proportions or correlations or odds ratios or any other numerical summary of the population. The alternative hypothesis is typically the research hypothesis of interest. Here are some examples.
Example 10.2: Hypotheses with One Sample of One Categorical Variable Section
About 10% of the human population is left-handed. Suppose a researcher at Penn State speculates that students in the College of Arts and Architecture are more likely to be left-handed than people found in the general population. We only have one sample since we will be comparing a population proportion based on a sample value to a known population value.
- Research Question : Are artists more likely to be left-handed than people found in the general population?
- Response Variable : Classification of the student as either right-handed or left-handed
State Null and Alternative Hypotheses
- Null Hypothesis : Students in the College of Arts and Architecture are no more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Art and Architecture = 10% or p = .10).
- Alternative Hypothesis : Students in the College of Arts and Architecture are more likely to be left-handed than people in the general population (population percent of left-handed students in the College of Arts and Architecture > 10% or p > .10). This is a one-sided alternative hypothesis.
Example 10.3: Hypotheses with One Sample of One Measurement Variable Section

A generic brand of the anti-histamine Diphenhydramine markets a capsule with a 50 milligram dose. The manufacturer is worried that the machine that fills the capsules has come out of calibration and is no longer creating capsules with the appropriate dosage.
- Research Question : Does the data suggest that the population mean dosage of this brand is different than 50 mg?
- Response Variable : dosage of the active ingredient found by a chemical assay.
- Null Hypothesis : On the average, the dosage sold under this brand is 50 mg (population mean dosage = 50 mg).
- Alternative Hypothesis : On the average, the dosage sold under this brand is not 50 mg (population mean dosage ≠ 50 mg). This is a two-sided alternative hypothesis.
Example 10.4: Hypotheses with Two Samples of One Categorical Variable Section

Many people are starting to prefer vegetarian meals on a regular basis. Specifically, a researcher believes that females are more likely than males to eat vegetarian meals on a regular basis.
- Research Question : Does the data suggest that females are more likely than males to eat vegetarian meals on a regular basis?
- Response Variable : Classification of whether or not a person eats vegetarian meals on a regular basis
- Explanatory (Grouping) Variable: Sex
- Null Hypothesis : There is no sex effect regarding those who eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis = population percent of males who eat vegetarian meals on a regular basis or p females = p males ).
- Alternative Hypothesis : Females are more likely than males to eat vegetarian meals on a regular basis (population percent of females who eat vegetarian meals on a regular basis > population percent of males who eat vegetarian meals on a regular basis or p females > p males ). This is a one-sided alternative hypothesis.
Example 10.5: Hypotheses with Two Samples of One Measurement Variable Section

Obesity is a major health problem today. Research is starting to show that people may be able to lose more weight on a low carbohydrate diet than on a low fat diet.
- Research Question : Does the data suggest that, on the average, people are able to lose more weight on a low carbohydrate diet than on a low fat diet?
- Response Variable : Weight loss (pounds)
- Explanatory (Grouping) Variable : Type of diet
- Null Hypothesis : There is no difference in the mean amount of weight loss when comparing a low carbohydrate diet with a low fat diet (population mean weight loss on a low carbohydrate diet = population mean weight loss on a low fat diet).
- Alternative Hypothesis : The mean weight loss should be greater for those on a low carbohydrate diet when compared with those on a low fat diet (population mean weight loss on a low carbohydrate diet > population mean weight loss on a low fat diet). This is a one-sided alternative hypothesis.
Example 10.6: Hypotheses about the relationship between Two Categorical Variables Section
- Research Question : Do the odds of having a stroke increase if you inhale second hand smoke ? A case-control study of non-smoking stroke patients and controls of the same age and occupation are asked if someone in their household smokes.
- Variables : There are two different categorical variables (Stroke patient vs control and whether the subject lives in the same household as a smoker). Living with a smoker (or not) is the natural explanatory variable and having a stroke (or not) is the natural response variable in this situation.
- Null Hypothesis : There is no relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is = 1).
- Alternative Hypothesis : There is a relationship between whether or not a person has a stroke and whether or not a person lives with a smoker (odds ratio between stroke and second-hand smoke situation is > 1). This is a one-tailed alternative.
This research question might also be addressed like example 11.4 by making the hypotheses about comparing the proportion of stroke patients that live with smokers to the proportion of controls that live with smokers.
Example 10.7: Hypotheses about the relationship between Two Measurement Variables Section
- Research Question : A financial analyst believes there might be a positive association between the change in a stock's price and the amount of the stock purchased by non-management employees the previous day (stock trading by management being under "insider-trading" regulatory restrictions).
- Variables : Daily price change information (the response variable) and previous day stock purchases by non-management employees (explanatory variable). These are two different measurement variables.
- Null Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) = 0.
- Alternative Hypothesis : The correlation between the daily stock price change (\$) and the daily stock purchases by non-management employees (\$) > 0. This is a one-sided alternative hypothesis.
Example 10.8: Hypotheses about comparing the relationship between Two Measurement Variables in Two Samples Section
- Research Question : Is there a linear relationship between the amount of the bill (\$) at a restaurant and the tip (\$) that was left. Is the strength of this association different for family restaurants than for fine dining restaurants?
- Variables : There are two different measurement variables. The size of the tip would depend on the size of the bill so the amount of the bill would be the explanatory variable and the size of the tip would be the response variable.
- Null Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the same at family restaurants as it is at fine dining restaurants.
- Alternative Hypothesis : The correlation between the amount of the bill (\$) at a restaurant and the tip (\$) that was left is the difference at family restaurants then it is at fine dining restaurants. This is a two-sided alternative hypothesis.
Statistics Tutorial
Descriptive statistics, inferential statistics, stat reference, statistics - hypothesis testing a proportion.
A population proportion is the share of a population that belongs to a particular category .
Hypothesis tests are used to check a claim about the size of that population proportion.
Hypothesis Testing a Proportion
The following steps are used for a hypothesis test:
- Check the conditions
- Define the claims
- Decide the significance level
- Calculate the test statistic
For example:
- Population : Nobel Prize winners
- Category : Born in the United States of America
And we want to check the claim:
" More than 20% of Nobel Prize winners were born in the US"
By taking a sample of 40 randomly selected Nobel Prize winners we could find that:
10 out of 40 Nobel Prize winners in the sample were born in the US
The sample proportion is then: \(\displaystyle \frac{10}{40} = 0.25\), or 25%.
From this sample data we check the claim with the steps below.
1. Checking the Conditions
The conditions for calculating a confidence interval for a proportion are:
- The sample is randomly selected
- Being in the category
- Not being in the category
- 5 members in the category
- 5 members not in the category
In our example, we randomly selected 10 people that were born in the US.
The rest were not born in the US, so there are 30 in the other category.
The conditions are fulfilled in this case.
Note: It is possible to do a hypothesis test without having 5 of each category. But special adjustments need to be made.
2. Defining the Claims
We need to define a null hypothesis (\(H_{0}\)) and an alternative hypothesis (\(H_{1}\)) based on the claim we are checking.
The claim was:
In this case, the parameter is the proportion of Nobel Prize winners born in the US (\(p\)).
The null and alternative hypothesis are then:
Null hypothesis : 20% of Nobel Prize winners were born in the US.
Alternative hypothesis : More than 20% of Nobel Prize winners were born in the US.
Which can be expressed with symbols as:
\(H_{0}\): \(p = 0.20 \)
\(H_{1}\): \(p > 0.20 \)
This is a ' right tailed' test, because the alternative hypothesis claims that the proportion is more than in the null hypothesis.
If the data supports the alternative hypothesis, we reject the null hypothesis and accept the alternative hypothesis.
Advertisement
3. Deciding the Significance Level
The significance level (\(\alpha\)) is the uncertainty we accept when rejecting the null hypothesis in a hypothesis test.
The significance level is a percentage probability of accidentally making the wrong conclusion.
Typical significance levels are:
- \(\alpha = 0.1\) (10%)
- \(\alpha = 0.05\) (5%)
- \(\alpha = 0.01\) (1%)
A lower significance level means that the evidence in the data needs to be stronger to reject the null hypothesis.
There is no "correct" significance level - it only states the uncertainty of the conclusion.
Note: A 5% significance level means that when we reject a null hypothesis:
We expect to reject a true null hypothesis 5 out of 100 times.
4. Calculating the Test Statistic
The test statistic is used to decide the outcome of the hypothesis test.
The test statistic is a standardized value calculated from the sample.
The formula for the test statistic (TS) of a population proportion is:
\(\displaystyle \frac{\hat{p} - p}{\sqrt{p(1-p)}} \cdot \sqrt{n} \)
\(\hat{p}-p\) is the difference between the sample proportion (\(\hat{p}\)) and the claimed population proportion (\(p\)).
\(n\) is the sample size.
In our example:
The claimed (\(H_{0}\)) population proportion (\(p\)) was \( 0.20 \)
The sample size (\(n\)) was \(40\)
So the test statistic (TS) is then:
\(\displaystyle \frac{0.25-0.20}{\sqrt{0.2(1-0.2)}} \cdot \sqrt{40} = \frac{0.05}{\sqrt{0.2(0.8)}} \cdot \sqrt{40} = \frac{0.05}{\sqrt{0.16}} \cdot \sqrt{40} \approx \frac{0.05}{0.4} \cdot 6.325 = \underline{0.791}\)
You can also calculate the test statistic using programming language functions:
With Python use the scipy and math libraries to calculate the test statistic for a proportion.
With R use the built-in prop.test() function to calculate the test statistic for a proportion.
5. Concluding
There are two main approaches for making the conclusion of a hypothesis test:
- The critical value approach compares the test statistic with the critical value of the significance level.
- The P-value approach compares the P-value of the test statistic and with the significance level.
Note: The two approaches are only different in how they present the conclusion.
The Critical Value Approach
For the critical value approach we need to find the critical value (CV) of the significance level (\(\alpha\)).
For a population proportion test, the critical value (CV) is a Z-value from a standard normal distribution .
This critical Z-value (CV) defines the rejection region for the test.
The rejection region is an area of probability in the tails of the standard normal distribution.
Because the claim is that the population proportion is more than 20%, the rejection region is in the right tail:
Choosing a significance level (\(\alpha\)) of 0.05, or 5%, we can find the critical Z-value from a Z-table , or with a programming language function:
Note: The functions find the Z-value for an area from the left side.
To find the Z-value for a right tail we need to use the function on the area to the left of the tail (1-0.05 = 0.95).
With Python use the Scipy Stats library norm.ppf() function find the Z-value for an \(\alpha\) = 0.05 in the right tail.
With R use the built-in qnorm() function to find the Z-value for an \(\alpha\) = 0.05 in the right tail.
Using either method we can find that the critical Z-value is \(\approx \underline{1.6449}\)
For a right tailed test we need to check if the test statistic (TS) is bigger than the critical value (CV).
If the test statistic is bigger than the critical value, the test statistic is in the rejection region .
When the test statistic is in the rejection region, we reject the null hypothesis (\(H_{0}\)).
Here, the test statistic (TS) was \(\approx \underline{0.791}\) and the critical value was \(\approx \underline{1.6449}\)
Here is an illustration of this test in a graph:
Since the test statistic was smaller than the critical value we do not reject the null hypothesis.
This means that the sample data does not support the alternative hypothesis.
And we can summarize the conclusion stating:
The sample data does not support the claim that "more than 20% of Nobel Prize winners were born in the US" at a 5% significance level .
The P-Value Approach
For the P-value approach we need to find the P-value of the test statistic (TS).
If the P-value is smaller than the significance level (\(\alpha\)), we reject the null hypothesis (\(H_{0}\)).
The test statistic was found to be \( \approx \underline{0.791} \)
For a population proportion test, the test statistic is a Z-Value from a standard normal distribution .
Because this is a right tailed test, we need to find the P-value of a Z-value bigger than 0.791.
We can find the P-value using a Z-table , or with a programming language function:
Note: The functions find the P-value (area) to the left side of Z-value.
To find the P-value for a right tail we need to subtract the left area from the total area: 1 - the output of the function.
With Python use the Scipy Stats library norm.cdf() function find the P-value of a Z-value bigger than 0.791:
With R use the built-in pnorm() function find the P-value of a Z-value bigger than 0.791:
Using either method we can find that the P-value is \(\approx \underline{0.2145}\)
This tells us that the significance level (\(\alpha\)) would need to be bigger than 0.2145, or 21.45%, to reject the null hypothesis.
This P-value is bigger than any of the common significance levels (10%, 5%, 1%).
So the null hypothesis is kept at all of these significance levels.
The sample data does not support the claim that "more than 20% of Nobel Prize winners were born in the US" at a 10%, 5%, or 1% significance level .
Note: It may still be true that the real population proportion is more than 20%.
But there was not strong enough evidence to support it with this sample.
Calculating a P-Value for a Hypothesis Test with Programming
Many programming languages can calculate the P-value to decide outcome of a hypothesis test.
Using software and programming to calculate statistics is more common for bigger sets of data, as calculating manually becomes difficult.
The P-value calculated here will tell us the lowest possible significance level where the null-hypothesis can be rejected.
With Python use the scipy and math libraries to calculate the P-value for a right tailed hypothesis test for a proportion.
Here, the sample size is 40, the occurrences are 10, and the test is for a proportion bigger than 0.20.
With R use the built-in prop.test() function find the P-value for a right tailed hypothesis test for a proportion.
Note: The conf.level in the R code is the reverse of the significance level.
Here, the significance level is 0.05, or 5%, so the conf.level is 1-0.05 = 0.95, or 95%.
Left-Tailed and Two-Tailed Tests
This was an example of a right tailed test, where the alternative hypothesis claimed that parameter is bigger than the null hypothesis claim.
You can check out an equivalent step-by-step guide for other types here:
- Left-Tailed Test
- Two-Tailed Test

COLOR PICKER

Contact Sales
If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]
Report Error
If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]
Top Tutorials
Top references, top examples, get certified.

IMAGES
COMMENTS
If the null hypothesis is true (the proportion is 0.25), then there is a 0.0103 probability that the sample (estimated) proportion is 0.4048 \(\left(\frac{17}{42}\right)\) or more. Use the previous information to sketch a picture of this situation. CLEARLY, label and scale the horizontal axis and shade the region(s) corresponding to the \(p ...
Null Hypothesis H 0: Group proportions are equal in the population: p 1 = p 2. Alternative Hypothesis H A: Group proportions are not equal in the population: p 1 ≠ p 2. Correlation and Regression Coefficients. Some studies assess the relationship between two continuous variables rather than differences between groups.
Null hypothesis (H 0): There's no effect in the population. Alternative hypothesis ... Two-proportions z test: The proportion of people with depression in the daily-meditation group (p 1) is greater than or equal to the no-meditation group (p 2) in the population; p 1 ≥ p 2.
It is the opposite of your research hypothesis. The alternative hypothesis--that is, the research hypothesis--is the idea, phenomenon, observation that you want to prove. If you suspect that girls take longer to get ready for school than boys, then: Alternative: girls time > boys time. Null: girls time <= boys time.
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
Hypothesis Test for Proportions: Step 3 •Calculate Test Statistic, z* •The test statistic measures how different the sample proportion we have is from the null hypothesis •We calculate the z-score by assuming that is the population proportion 𝑧∗= ( − ) 1− 8
For a test for two proportions, we are interested in the difference between two groups. If the difference is zero, then they are not different (i.e., they are equal). Therefore, the null hypothesis will always be: H 0: p 1 − p 2 = 0. Another way to look at it is H 0: p 1 = p 2.
That is, we reject the null hypothesis \(H_0\) if \(Z ≥ 1.96\) or if \(Z ≤ −1.96\). We clearly reject \(H_0\), since 8.99 falls in the "red zone," that is, 8.99 is (much) greater than 1.96. There is sufficient evidence at the 0.05 level to conclude that the two populations differ with respect to their opinions concerning imposing a ...
The first step is to state the null hypothesis and an alternative hypothesis. Null hypothesis: P = 0.80. Alternative hypothesis: P ≠ 0.80. Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the sample proportion is too big or if it is too small. Formulate an analysis plan. For this analysis, the ...
In hypothesis testing, we assume the null hypothesis is true. Remember, we set up the null hypothesis as H 0: p = p 0. This is very important! This statement says that we are assuming the unknown population proportion, p, is equal to the value p 0. Since this is true, then we can follow the same logic above. Therefore, if n p 0 and n ( 1 − p ...
Null hypothesis (H 0): There's no effect in the population. Alternative hypothesis ... Two-proportions z test: The proportion of people with depression in the daily-meditation group (p 1) is less than the no-meditation group (p 2) in the population; p 1 < p 2. Differences between null and alternative hypotheses.
This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.93[/latex]. The p-value of 0.2710 tells us that under the assumption that 93% of visitors make a purchase (the null hypothesis), there is a 27.10% chance that the number of visitors in a sample of 50 who make a purchase is 45 or ...
Our alternative hypothesis is based on a theory that internet access has become more available. Quote: "...want to test if that proportion is now higher". Meaning, alternative hypothesis is p > 0.9, not p ≠ 0.9. We do not know why the researchers had that theory, our hypothesis testing is simply based on the data presented.
Hypothesis testing is a decision-making process by which we analyze a sample in an attempt to distinguish between results that can easily occur and results that are unlikely. One begins with a claim or statement -- the reason for the study. For example, the claim might be "This coin in my pocket is fair." Then we design a study to test the ...
Step 1: Determine the hypotheses. The hypotheses are claims about the population proportion, p. The null hypothesis is a hypothesis that the proportion equals a specific value, p0. The alternative hypothesis is the competing claim that the parameter is less than, greater than, or not equal to p0. Step 2: Collect the data.
The test looks at the proportion (p) of individuals in the population who have a certain characteristic — for example, the proportion of people who carry cellphones.The null hypothesis is H 0: p = p 0, where p 0 is a certain claimed value of the population proportion, p.For example, if the claim is that 70% of people carry cellphones, p 0 is 0.70. The alternative hypothesis is one of the ...
In the computation of σ, Sal observes that because the premise of the hypothesis test is that the null hypothesis is true, we assume that p^_2015 = p^_2000 and thus use the combined p^_c as the basis for a "best estimate" of σ.This I understand and concur with. However, it's not clear to me why the numerator for computing z is p^_2015 - p^_2000 rather than p^_2015 - p^_c.
Remember the 𝒛 for any test statistic is =. (Estimator﹣Null) / SE. Let's focus on the numerator (Estimator﹣Null): ∙ The "estimator" in this case is the difference between proportions. This is what we are trying to estimate from the question. Thus, Estimator = p̂₁﹣ p̂₂. ∙ The "null" in this case is zero.
The alternative hypothesis ( Ha H a) is a claim about the population that is contradictory to H0 H 0 and what we conclude when we reject H0 H 0. Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample ...
10.1 - Setting the Hypotheses: Examples. A significance test examines whether the null hypothesis provides a plausible explanation of the data. The null hypothesis itself does not involve the data. It is a statement about a parameter (a numerical characteristic of the population). These population values might be proportions or means or ...
H 0 (Null Hypothesis): Population parameter =, ≤, ≥ some value. H A (Alternative Hypothesis): Population parameter <, >, ≠ some value. Note that the null hypothesis always contains the equal sign. We interpret the hypotheses as follows: Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.
4. Calculating the Test Statistic. The test statistic is used to decide the outcome of the hypothesis test. The test statistic is a standardized value calculated from the sample. The formula for the test statistic (TS) of a population proportion is: p ^ − p p ( 1 − p) ⋅ n.
The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise.. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength ...