mathematical problem solving routine

Fun teaching resources & tips to help you teach math with confidence

Simple Yet Powerful Math Number Sense Routine: Close, Far, In-Between

Looking for an easy way to weave daily number sense practice into your math routine? Learn what number sense routines are & get started with this simple number sense routine known as close, far or in-between.

Mathematics is often perceived as a daunting subject, filled with complex equations and abstract concepts. However, at its core, math is about understanding relationships, patterns, and making sense of the world around us. Number sense routines are a powerful tool for developing a deep and intuitive understanding of numbers , paving the way for mathematical success. In this blog post, we’ll explore what number sense routines are, why they matter, how they can benefit learners of all ages, and a freebie for one of my favorites: Close, Far, or In-Between Number Sense Routine . Read even more about the Close, Far, or In-Between Number Sense Routine HERE .

*This is a guest post from Danielle at Math MindED Teaching

What Are Number Sense Routines?

Number sense routines are short, structured activities designed to help individuals develop an intuitive understanding of numbers and their relationships.

These routines focus on fundamental mathematical concepts , such as counting, comparing, and estimating, and can be adapted for learners of all ages, from early childhood to adulthood.

Why Are Number Sense Routines Important?

• Build a Strong Foundation: Number sense is the foundation upon which more advanced mathematical concepts are built. Developing a strong number sense early in one’s mathematical journey can lead to better comprehension of higher-level math.
• Enhance Problem-Solving Skills: Number sense routines promote critical thinking and problem-solving abilities. When individuals have a deep understanding of numbers, they can tackle complex problems more effectively.
• Foster Mathematical Confidence: Math anxiety is a common issue among learners of all ages. Number sense routines provide a low-stress, enjoyable way to engage with math, helping individuals build confidence in their abilities.
• Real-Life Application: Number sense is not just confined to the classroom. It’s a skill that’s highly relevant in everyday life, from budgeting and cooking to making informed decisions based on data.
• Adaptability: Number sense routines can be tailored to suit the needs and abilities of learners at different levels, making them an excellent tool for both educators and self-learners.

Examples of Number Sense Routines

• Which One Doesn’t Belong? – Present a set of numbers or shapes and ask learners to identify which one doesn’t belong and explain their reasoning.
• Estimation Jar – Fill a jar with objects (e.g., marbles, beans) and ask learners to estimate how many are in the jar. Then, count to check their estimates.
• Number Talks – Engage in open-ended discussions about mathematical problems, encouraging learners to share their strategies and solutions.
• Number Strings –  A set of related math problems designed to teach strategies based on number relationships. It is a 10-15 minute routine that can be used for any math topic.
• Counting Collections – Gather a collection of objects and have learners count them in various ways (e.g., by twos, by fives, by tens).
• Counting Circles – Students stand and form a circle facing in toward each other. The teacher selects a counting sequence to practice. Children take turns counting a number one at a time around the circle. Count by whole numbers, fractions, or decimals!
• Choral Counting – Activity in which the teacher leads children in counting aloud together by a given number. As the class calls out each number the teacher records the count on the board, pausing the count at strategic moments and recording patterns. Again, you can count by whole numbers, fractions, or decimals!
• Mental Math Challenges – Pose simple addition, subtraction, multiplication, or division problems for learners to solve mentally within a time limit.
• Same or Different? –  A routine that provides students opportunities to construct arguments when comparing objects, such as numbers or shapes. Pictures can be strategically created to elicit strategy related mathematical discourse.
• Two Truths, One Lie – Students are presented with three facts, images, or statements (only two of which are true). The objective is for students to identify which statement is false and justify why.
• Missing Midpoint/Missing Endpoint – This routine involves a number line with two endpoints and a missing midpoint. This routine encourages students to find the midpoint by thinking about dividing the number line into equal parts.
• Close, Far, or In-Between – This activity focuses on number sense development and relative magnitude. When thinking about relative magnitude, students can compare and refer to the size relationship one number has with another.

Close, Far, or In-Between Number Sense Routine

For this routine, the teacher displays three numbers for students to review.

• For kindergarten students, use smaller numbers (0-10).
• For first and second graders, use 2 digit numbers.
• For third grade students, use 3 digit numbers or simple fractions.
• For fourth and fifth grade students use large numbers, fractions and decimals.
• For an extra challenge or for middle school students use positive/negative integers.

Then ask questions that encourage relative magnitude relations . Be sure to encourage mathematical discourse.

Some examples of questions to pose to your students:

• Which two are closest together?
• Which number is closest to 10? 50? 100? 500? etc.
• Name a number that is greater/less than all three
• Name a number (or fraction/decimal) between __ & __ (2 of the numbers)
• How far apart are __ & __? (2 of the numbers)

I love using Close, Far, or In-Between to teach DECIMAL understanding .

This number sense routine helps students to visually make sense of decimals on a number line .

Would you like a FREE Decimal version of the Close, Far, or In-Between Number Sense Routine? Check it out HERE .

Can’t get enough DECIMAL products for your students? Then check out these other DECIMAL resources for students in grades 4-6 .

Number sense routines are not just about crunching numbers ; they are about developing a deep and intuitive understanding of mathematics. These routines empower learners to see math as a language that helps them make sense of the world.

By incorporating number sense routines into our educational practices and daily lives, we can cultivate mathematical intuition, enhance problem-solving skills, and build a strong foundation for lifelong learning . So, whether you’re a teacher, a parent, or a lifelong learner, embrace number sense routines as a valuable tool on your mathematical journey .

Similar Posts

Grow a Christmas Tree Farm! {FREE Math Game}

{FREE} Candy Corn Counting: Printable Math Mats

Fun Thanksgiving Math & Logic Puzzles {FREE}

{FREE} Earth Day Geoboard Activity – Grades K-2

Valentine’s Day Tally, Count & Graph: Grades K-2

Multiply Decimals Classroom Scavenger Hunt {FREE}

Find more resources to help make math engaging, join 165k+ parents & teachers.

Who learn new tips and strategies, as well as receive engaging resources to make math fun!

• Privacy Policy

Math Time Doesn't Have to End in Tears

Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

--> -->

Trending Post : Easy Fixes for Behavior Challenges

5 Ways to Build Math Problem Solving Skills (based on brain research)

Whether talking about state tests or meeting with your team to plan the next math unit, the conversation inevitably turns to word problems. But knowing how to build math problem-solving skills without resorting to pages of boring story problem practice can be hard.

These days word problems aren’t the basic one-step wonders that many of us dealt with as students. Instead, multi-step story problems that require students to apply multiple concepts and skills are incorporated into instruction and state assessments.

Understanding brain research can help simply the process of teaching this challenging format of math problem-solving to students, including those who struggle.

What research says about building master problem solvers in math

Have you seen how many math skills we must teach these days? No teacher has enough time to build critical math skills AND effectively teach problem-solving…or do they?

Research would argue we are going about these tasks all wrong. They say there are many reasons students struggle with math word problems , but one big one is that we aren’t doing what’s best for the brain. Instead, here’s what the brain research says about the must-have elements for building step-by-step math problem-solving mastery.

Finding #1: Becoming a master problem solver requires repetition.

Duh, right? Any good teacher knows this…but what’s the best recipe for repetition if you want students to master math word problems? How much practice? How often?

Let’s start with the concept of mastery.

How do you develop math problem solving skills?

In the 1990’s, Anders Ericsson studied experts to explore what made some people excel. Findings showed a positive correlation between the amount of deliberate practice (activities that require a high level of concentration and aren’t necessarily inherently fun) and skill level.

In other words, the more practice someone gets, the more they improve. This became the basis of Malcolm Gladwell’s 10,000-hour rule, which stated that it takes 10,000 hours to make you an expert in a field.

But what should that practice look like for students who struggle with word problems? Is it better to have a deep dive into story problems, or do short bursts of practice do more for long-term understanding?

Designing Better Word Problem Activities: Building Step-by-step Math Problem-Solving Practice

We can look at Ebbinghaus’ work on memory & retention to answer that.  He found spacing practice over time decreased the number of exposures needed. In other words, small amounts of practice over several days, weeks, or even months actually means you need LESS practice than if you try to cram it all in at once.

For over 80 years, this finding has stood the test of time. While research has shown that students who engage in mass practice (lots of practice all at once) might do better on an assessment that takes place tomorrow, students who engage in repeated practice over a period of time retain more skills long-term (Bloom & Shuell, 1981; Rea & Modigliani, 1985).

And how long does the research say you should spend reviewing?

How long should problem-solving practice really be?

Shorter is better. As discussed earlier, peak attention required for deliberate practice can only be maintained for so long. And the majority of research supports 8-10 minutes as the ideal lesson length (Robertson, 2010).

This means practice needs to be focused so that during those minutes of discussion, you can dive deep – breaking down the word problem and discussing methods to solve it.

Teacher Tip: Applying this finding to your classroom

Less is actually more as long as you plan to practice regularly. While students who struggle with word problems may need a great deal of practice to master word problems, ideally, this practice should be provided in short, regular intervals with no more than 8-10 minutes spent in whole group discussion.

Here are a few simple steps to apply these findings to your math classroom:

• Find 8-12 minutes in your daily schedule to focus on problem-solving – consider this time sacred & only for problem-solving.
• Select only 1-2 word problems per day. Target step-by-step math problem-solving to build math problem-solving skills through a less-is-more approach using Problem of the Day .

Finding #2: Students who are challenged & supported have better outcomes.

Productive struggle, as it is called in the research, focuses on the effortful practice that builds long-term understanding.

Important to this process are opportunities for choice, collaboration, and the use of materials or topics of interest (which will be discussed later).

This productive struggle also helps students build flexible thinking so that they can apply previously learned skills to new or unfamiliar tasks (Bransford, Brown, & Cocking, 2000).

“Meaningful learning tasks need to challenge ever student in some way. It is crucial that no student be able to coast to success time after time; this experience can create the belief that you are smart only if you can succeed without effort.” -Carol Dweck

It is also critical to provide support and feedback during the challenging task (Cimpian, Arce, Markman, & Dweck, 2007). This prevents frustration and fear of failure when the goal seems out of reach or when a particularly challenging task arises.

Simple ways to build productive struggle into your math classroom

Giving students who struggle with word problems a chance to struggle with challenging word problems is critical to building confidence and skills. However, this challenge must be reasonable, or the learner’s self-esteem will falter, and students need support and regular feedback to achieve their potential.

Here are a few simple things to try:

• Select problems that are just at the edge of students’ Zone of Proximal Development.
• Scaffold or model with more challenging problems to support risk-taking.
• Give regular feedback & support – go over the work and discuss daily.

Finding #3: Novelty & variation are keys to engagement.

When it comes to standardized testing (and life in general), problems that arise aren’t labeled with the skills and strategies required to solve them.

This makes it important to provide mixed practice opportunities so students are focused on asking themselves questions about what the problem is asking and what they are trying to find.

This type of variation not only supports a deeper level of engagement, it also supports the metacognitive strategies needed to analyze and develop a strategy to solve (Rohrer & Taylor, 2014).

The benefits of novelty in learning

A 2013 study also supports the importance of novelty in supporting reinforcement learning (aka review). The findings suggested that when task variation was provided for an already familiar skill, it offered the following benefits:

• reduced errors due to lack of focus
• helped learners maintain attention to task
• motivated and engaged student

Using variety to build connections & deepen understanding

In addition, by providing variations in practice, we can also help learners understand the skills and strategies they are using on a deeper level.  

When students who struggle with word problems are forced to apply their toolbox of strategies to novel problem formats, they begin to analyze and observe patterns in how problems are structured and the meaning they bring.

This requires much more engagement than being handed a sheet full of multiplication story problems, where students can pull the numbers and compute with little focus on understanding.

Designing word problems that incorporate variety & novelty

Don’t be afraid to shake things up!

Giving students practice opportunities with different skills or problem formats mixed in is a great way to boost engagement and develop meta-cognitive skills.

Here are a few tips for trying it out in the classroom:

• Change it up! Word problem practice doesn’t have to match the day’s math lesson.
• Give opportunities to practice the same skill or strategy in via different formats.
• Adjust the wording and/or topic in word problems to help students generalize skills.

Finding #4: Interest and emotion increase retention and skill development.

Attention and emotion are huge for learning. We’ve all seen it in our classroom.

Those magical lessons that hook learners are the ones that stick with them for years to come, but what does the research say?

The Science Behind Emotion & Learning

Neuroscientists have shown that emotions create connections among different sections of the brain (Immordino-Yang, 2016) . This supports long-term retrieval of the skills taught and a deeper connection to the learning.

This means if you can connect problem-solving with a scenario or a feeling, your students will be more likely to internalize the skills being practiced. Whether this is by “wowing” them with a little-known fact or solving real-world problems, the emotional trigger can be huge for learning.

What about incorporating student interests?

As for student interests, a long line of research supports the benefits of using these to increase educational outcomes and student motivation, including for students who struggle with word problems (Chen, 2001; Chen & Ennis, 2004; Solomon, 1996).

Connecting classwork with student interests has increased students’ intentions to participate in future learning endeavors (Chen, 2001).

And interests don’t just mean that love of Pokemon!

It means allowing social butterflies to work collaboratively. Providing students with opportunities to manipulate real objects or create models. Allowing kids to be authentic while digging in and developing the skills they need to master their learning objectives.

What this looks like in a math class

Evoke emotion and use student interests to engage the brain in deep, long-lasting learning whenever possible.

This will help with today’s learning and promote long-term engagement, even when later practice might not be as interesting for students who struggle with word problems.

Here’s how to start applying this research today:

• Find word problems that match student interests.
• Connect real-life situations and emotions to story problem practice.
• Consider a weekly theme to connect practice throughout the week.

Finding #5: Student autonomy builds confidence & independence.

Autonomy is a student’s ability to be in control of their learning. In other words, it is their ability to take ownership over the learning process and how they demonstrate mastery.

Why students need to control their learning

Research shows that providing students a sense of control and supporting their choices is way to help engage learners and build independent thinking. It also increased intrinsic motivation (Reeve, Nix, & Hamm, 2003).

However, this doesn’t mean we just let kids learn independently. Clearly, some things require repeated guidance and modeling. Finding small ways that students can take control of the learning process is much better in these instances.

We know that giving at least partial autonomy has been linked to numerous positive student learning outcomes (Wielenga-Meijer, Taris, Widboldus, & Kompier, 2011).

But how can we foster this independence and autonomy, especially with those students who struggle to self-regulate behavior?

Fostering independence in students who struggle to stay on task

Well, the research says several conditions support building toward independence.

The first (and often neglected) is to explain unappealing choices and why they are one of the options.

When it comes to word problems, this might include explaining the rationale behind one of the strategies that appears to be a lot more work than the others.

It is also important to acknowledge students’ negative feelings about a task or their ability to complete it. While we want them to be able to build independence, we don’t want them to drown in overwhelm.

By providing emotional support, we can help determine whether a student is stuck with the learning or with the emotions from the cognitive challenge.

Finally, giving choices is recommended. Identifying choices you and your students who struggle with word problems can live with is an important step.

Whether this is working in partners, trying an alternative method, or skipping a problem and coming back, students need to feel like they have some ownership over the challenge they are working through.

By building in opportunities for autonomy, and choice, teachers help students build a sense of self-efficacy and confidence in their ability to be successful learners across various contexts (McCombs, 2002,2006).

We know this leads to numerous positive outcomes and has even been linked to drop-out prevention (Christenson & Thurlow, 2004).

Fostering autonomy in your classroom

You’re not going to be able to hold their hands forever.

Giving opportunities to work through challenges independently and to feel ownership for their choices will help build both confidence and skills.

Here’s how to get started letting go:

• Give students time to tackle the problem independently (or in partners).
• Don’t get hyper-focused on a single method to solve – give opportunities to share & learn together.
• Provide appropriate support (where needed) to build autonomy for all learners – like reading the problem orally.

Finding #6: Students need to be taught how to fail & recover from it.

Despite Ericsson’s findings discussed early on in this post, talent does matter, and it is important to teach students to recover from failure because those are the moments when they learn the most.

A 2014 study by Brooke Macnamara analyzed 88 studies to determine how talent factored into deliberate practice.

Her findings show what we (as teachers) already know, students may require different amounts of practice to reach the same skill level…but how do we keep those struggling students from keeping up?

Growth mindset research gives us insight into ways to support students who struggle with word problems, encourage all students in math problem-solving, and harness the power of failure through “yet.”

You might not be able to do something yet, but if you keep trying, you will. This opens the door for multiple practice opportunities where students learn from each other.

And what about the advanced students?

Many of these students have not experienced failure, but they may have met their match when it comes to complex word problems.

To support these students, who may be experiencing their first true challenge, we need to have high standards and provide constructive, supportive feedback on how to grow.

Then we need to give them space to try again.

There is great power in allowing students to revise and try again, but our grading system often discourages being comfortable with failure.

Building the confidence to fail in your classroom

Many students feel the pressure always to have the right answer. Allowing students to fail safely means you can help them learn from these failures so they don’t make the same mistake twice.

Here’s how you can safely foster growth and build math problem solving skills through failure in your classroom:

• Build in time to analyze errors & reflect.
• Reward effort & growth as much as, if not more than, accuracy.
• ​At least initially, skip the grading so students aren’t afraid to be wrong.

Getting started with brain-based problem solving

The brain research is clear.

Spending 45 minutes focused on a sheet of word problems following the same format isn’t the answer.

By implementing this research, you can save yourself time and the frustration from a disengaged class.

Based on this research, I’ve created Daily Problem Solving bundles to save you time and build math problem-solving skills. You can get each month separately or buy the full-year bundle at a major discount.

Currently, I offer these bundles for several grade levels, including:

Try Daily Problem Solving with your Learners

Of course, you do! Start working to build step-by-step math problem-solving skills today by clicking the button below to sign up for a free set of Daily Problem Solving.

Similar Posts

The Easy Way to Teach Place Value to Help Struggling Learners

30+ Awesome Online Games for Math Fact Practice

5 Engaging Ideas for Teaching Math with Video

Must-Have Math Manipulatives for Conceptualizing Place Value

Supporting Reluctant Learners with Math Anxiety

How to Simplify Addition with Regrouping to Help Struggling Learners

Leave a reply cancel reply.

You must be logged in to post a comment.

• Inside Mathematics
• Math Pathways (DCMP)
• Keywords Search
• inside problem solving

Inside Problem Solving

The Inside Problem Solving problems are non-routine math problems designed to promote problem-solving in your classroom. Each problem is divided into five levels of difficulty, Level A through Level E, to allow access and scaffolding for students into different aspects of the problem and to stretch students to go deeper into mathematical complexity. The problems were developed by the Silicon Valley Mathematics Initiative and are aligned to the Common Core standards.

To request the Inside Problem Solving Solutions Guide, please get in touch with us via the feedback form .

Courtney’s Collection   Cut It Out Cutting a Cube Digging Dinosaurs Diminishing Return First Rate Friends You Can Count On Game Show Got Your Number Growing Staircases Measuring Mammals Measuring Up Miles of Tiles Movin ‘n Groovin On Balance Once Upon A Time Part and Whole Party Time Piece it Together Polly Gone Rod Trains Surrounded and Covered Squirreling It Away The Shape of Things The Wheel Shop Through the Grapevine Tri-Triangles What’s Your Angle?

Cutting a Cube (K.G.B.4) Digging Dinosaurs (K.OA.A.2) First Rate (K.CC.B.5, K.CC.C.6) Growing Staircases (K.CC.B.5) On Balance (K.MD.A.2)

Cutting a Cube (1.G.A.1) Growing Staircases (1.OA.A.1) Rod Trains (1.MD.A.2, 1.OA.C.6) Measuring Mammals (1.MD.A.1) Miles of Tiles (1.OA.A.1) Movin ‘n Groovin (1.OA.A.1) Piece it Together (1.G.A.2)

Courtney’s Collection (2.MD.C.8) Digging Dinosaurs (2.MD.C.8) Got Your Number (2.OA.B.2, 2.NBT.A.1, 2.NBT.A.4, 2.NBT.B.5) Miles of Tiles (2.NBT.B.5) Part and Whole (2.G.A.3) Piece it Together (2.G.A.1) Squirreling It Away (2.OA.1) The Shape of Things (2.G.A.1) Through the Grapevine (2.MD.D.9, 2.MD.D.10) What’s Your Angle? (2.G.A.1)

Measuring Up (3.OA.A.3) Once Upon A Time (3.MD.A.1) Part and Whole (3.G.A.2, 3.NF.A.1, 3.MD.C.6) Party Time (3.OA.A.3) Piece it Together (3.MD.C.5, 3.MD.D.8) Polly Gone (3.MD.D.8) Surrounded and Covered (3.MD.C.6, 3.MD.D.8) The Wheel Shop (3.OA.A.1, 3.OA.A.2) Tri-Triangles (3.OA.A.3)

Courtney’s Collection (4.MD.A.2) Digging Dinosaurs (4.MD.A.2) Diminishing Return (4.OA.A.3, 4.MD.A.2) Friends You Can Count On (4.OA.A.3) Game Show (4.OA.C.5) Growing Staircases (4.OA.C.5) Measuring Mammals (4.OA.A.2) Measuring Up (4.OA.A.3) Once Upon A Time (4.OA.A.3) Part and Whole (4.G.A.3) Party Time (4.NF.B.4c) Piece it Together (4.G.A.2, 4.MD.C.6) Squirreling It Away (4.OA.3) The Shape of Things (4.G.A.3) The Wheel Shop (4.OA.A.3) Tri-Triangles (4.OA.C.5)

Digging Dinosaurs (5.NBT.B.7) Movin ‘n Groovin (5.NF.B.4)

Courtney’s Collection (6.NS.B.4) Cutting a Cube (6.G.A.4, 6.RP.A.3c) Diminishing Return (6.RP.A.3a, 6.RP.A.3b) First Rate (6.RP.A.3b, 6.RP.A.2) Measuring Up (6.RP.A.3c, 6.EE.A.1, 6.EE.B.7) On Balance (6.EE.B.5, 6.EE.B.6, 6.EE.B.8) Once Upon A Time (6.NS.B.2, 6.NS.B.4) Movin ‘n Groovin (6.RP.A.3d) Part and Whole (6.G.A.1) Piece it Together (6.G.A.4) Polly Gone (6.G.A.1) Surrounded and Covered (6.RP.A.2, 6.RP.A.3b) Tri-Triangles (6.EE.A.1, 6.EE.B.6, 6.EE.C.9)

Courtney’s Collection (7.SP.C.8b) First Rate (7.RP.A.2b, 7.RP.A.3, 7.EE.B.4a) Friends You Can Count On (7.SP.C.7a, 7.SP.C.8a, 7.SP.C.8b) Game Show (7.SP.C.8a, 7.SP.C.8b) Got Your Number (7.NS.A.3) Measuring Mammals (7.RP.A.2a, 7.RP.A.2b, 7.RP.A.2c 7.RP.A.1) Measuring Up (7.RP.A.2b, 7.RP.A.2c, 7.RP.A.3, 7.EE.B.4) Movin ‘n Groovin (7.RP.A.2c, 7.RP.A.3) Part and Whole (7.NS.A.1D) Piece it Together (7.G.B.6) Polly Gone (7.G.B.6, 7.G.B.4) Rod Trains (7.SP.C.8b) Squirreling It Away (7.SP.8b) Surrounded and Covered (7.G.B.4, 7.G.B.6) Through the Grapevine (7.SP.A.2)

Cutting a Cube (8.G.A.1a) Digging Dinosaurs (8.EE.C.7b, 8.F.B.4) Diminishing Return (8.EE.C.7.b) Miles of Tiles (8.EE.C.8b, 8.EE.C.8c) Movin ‘n Groovin (8.EE.B5) On Balance (8.EE.C.8b, 8.EE.C.8c) Once Upon A Time (8.EE.C.8b) Squirreling It Away (8-F.1) Through the Grapevine (8.SP.A.1, 8.SP.A.2) The Wheel Shop (8.EE.C.8b, 8.EE.C.8c)

Courtney’s Collection (A-CED.A.2) Digging Dinosaurs (A-CED.A.2) Diminishing Return (A-CED.A.1) Growing Staircases (A-CED.A.2) Measuring Mammals (A-CED.A.2, A-REI.B.3, A-REI.C.6) Measuring Up (A-CED.2) Miles of Tiles (A-APR.A.1, A-SSE.A.1a, A-SSE.A.2) On Balance (A-CED.A.2, A-REI.C.6) Once Upon A Time (A-CED.A.1) Part and Whole (A-APR.D.6) Polly Gone (A-REI.C.6) Squirreling It Away (A-CED.2, A-CED.3, A-REI.6, A-REI.8, A-REI.10) The Wheel Shop (A-REI.C.6, A-REI.D.12) Tri-Triangles (A-CED.A.1, A-REI.B.4b, A-SSE.A.2)

Cut It Out (F-BF.A.1a) Digging Dinosaurs (F-IF.C.7b, F-IF.C.7e) Diminishing Return (F-BF.A.1a) First Rate (F-IF.B.6, F-BF.A.1a) Growing Staircases (F-LE.A.2, F-BF.A.2, F-BF.A.1a) Movin ‘n Groovin (F.BF. A.1a) Rod Trains (F-BF.A.1a) Squirreling It Away (F.LE.2, F-BF.1a, F-BF.2) Surrounded and Covered (F-BF.A.1a) Tri-Triangles (F-BF.A.1a) What’s Your Angle? (F-BF.A.1a)

Cut It Out (G-CO.B.6) Growing Staircases (G-MG.1) First Rate (G-SRT.C.8) Measuring Mammals (G-SRT.B.5) Miles of Tiles (G-MG.A.3) Once Upon A Time (G-C.A.2) Piece it Together (G.MG.A.1, G-MG.A.3, G.GMD.A.1, G.SRT.C.8) Polly Gone (G-CO.B.7, G-GPE.B.7, G-MG.A.3, G-GPE.B.4) The Shape of Things (G-C.A.2, G-CO.C.10, G-CO.C.11, G-SRT.B.5, G-MG.A.1) What’s Your Angle? (G-MG.A.3, G-C.A.2)

Digging Dinosaurs (S-ID.6.a) Diminishing Return (S-CP.A.2, S-CP.B.8) Friends You Can Count On (S-CP.A.4, S-CP.A.5, S-CP.B.6) Game Show (S-MD.A.1, S-MD.A.2, S-MD.A.3) Growing Staircases (S-ID.6a) Party Time (S-CP.A.1, S-CP.B.9, S-CP.B.8) Squirreling It Away (S-ID.6a) Through the Grapevine (S-IC.B.4, S-ID.A.1, S-ID.A.2, S-ID.A.3, S-ID.B.5, S-ID.B.6c) The Wheel Shop (S-CP.A.1)

Why Problem Solving?

Problem solving is the cornerstone of doing mathematics. George Polya, a famous mathematician from Stanford, once said, "A problem is not a problem if you can solve it in 24 hours." His point was that a problem that you can solve in less than a day is usually a problem that is similar to one that you have solved before, or at least is one where you recognize that a certain approach would lead to the solution. Bu t in real life, a problem is a situation that confronts you and you don’t have an idea of where to even start. Mathematics is the toolbox that solves so many problems. Whether it is calculating an estimate measure, modeling a complex situation, determining the probability of a chance event, transforming a graphical image or proving a case using deductive reasoning, mathematics is used. If we want our student s to be problem solvers and mathematically powerful, we must model perseverance and challenge students with non-routine problems.

Change location

• Connecticut
• District of Columbia
• Massachusetts
• Mississippi
• New Hampshire
• North Carolina
• North Dakota
• Pennsylvania
• Puerto Rico
• Rhode Island
• South Carolina
• South Dakota
• West Virginia
• Contact Sales

LITERACY SUITE

• SCIENCE OF READING PROGRAMS
• Amplify CKLA (PreK–5)
• Boost Reading (K–5)
• mCLASS (K–6)
• mCLASS Intervention (K–6)
• Amplify Tutoring (K–6)
• SPANISH LITERACY PROGRAMS
• Amplify Caminos (K–5)
• Boost Lectura (K–2)
• mCLASS Lectura (K–6)
• MIDDLE SCHOOL PROGRAMS
• Amplify ELA (6–8)
• Boost Close Reading (6–8)

MATH & SCIENCE SUITE

• MATH PROGRAMS
• Amplify Desmos Math (K–A2)
• Desmos Math 6–A1
• mCLASS Math (K–3)
• MATH PLATFORM
• Desmos Classroom (K–12)
• SCIENCE PROGRAM
• Amplify Science (PreK–8)

High-Quality Materials

• STIMULUS HUB
• 5 Fundamentals
• Amplify on EdReports
• Science of Reading podcast
• Science of Reading resource Site
• Dyslexia and the Science of Reading
• Teacher-administered assessment
• Principles of Middle School ELA
• Math Teacher Lounge podcast
• Desmos Classroom
• Future of Math
• Social, problem-based math
• 5 Practices research findings
• Science Connections podcast
• Phenomena-based learning
• Literacy-rich instruction
• Science blog
• Science success stories
• RESEARCH HUB
• Amplify CKLA & Amplify Caminos
• Amplify ELA
• Amplify Science
• Boost Reading & Boost Lectura
• mCLASS & mCLASS Lectura
• Amplify Tutoring

Blog and webinar library

• Literacy blog
• Webinar library
• Literacy webinar library
• Math webinar library
• Science webinar library

Media & events

• Podcast hub
• PRESS RELEASES
• Media highlights
• Upcoming events
• Ordering and payment
• Amplify science - Randome search result

Daily math routines that spark student curiosity

Classroom routines can build creativity and community. Find out how.

It’s the educator’s eternal question: How do I keep students engaged?

When designing daily math practice, teachers are always working to make real-world math problems fresh and relevant, find new entrance points for concepts, or simply come up with surprises. All of these approaches can be very effective.

And though it may seem counter-intuitive, so can routines.

The power of instructional routine

The word routine can connote a sense of doing something mechanically, even without thinking. But teachers know that well-placed classroom routines can open opportunities for creative thought.

Routines provide a way for you and your students to build and maintain a sense of familiarity and structure throughout the school year. They also free up time teachers would otherwise spend giving directions. When students know exactly how a certain activity should run, and understand all instructions and expectations, everything goes more smoothly.

That’s why a core set of shared routines can be a powerful, practical force for establishing an effective classroom learning community..

Bringing math routine into the classroom

We know routines can be effective in any classroom. Now, we also have research offering direct evidence that certain routines are particularly effective in math classrooms.

Think-pair-share

Do you want your students to have more time to think before solving and sharing about a problem? 

GOAL: Provides opportunities to identify, compare, and contrast multiple strategies

TIP: During partnered discussion, consider displaying sentence frames such as, “ First they… Next they…” “Their strategy was to…” or “I see a/an… in both strategies.”.

How to do it:

• Invite students to solve a problem that can be solved with multiple strategies. Then, display two or more different responses representing different strategies.
• Give students time to analyze the strategies on their own and then invite them to discuss them with a partner.
• Facilitate a class discussion to describe, compare, contrast, and connect the different strategies. Utilize open-ended questions like, “Why did different strategies lead to the same outcome?” or, “What was helpful about each strategy?”

Where to learn more

We worked with our curriculum team to develop routine cards for math teachers, so you can implement routines that are part of our math program in your classroom. Most of the routines you’ll find throughout Amplify Desmos Math have been specifically proven effective in math classrooms. All of them have been adapted from established teaching practices.

We invite you to access a sample set of some of our most popular routines and decide which ones to try out in your classroom!

Download free math instructional routine cards .

Explore Desmos Classroom .

Learn more about Amplify Desmos Math .

Stay in touch

Related resources.

Amplify Desmos Math

Amplify Desmos Math: Bringing you free tools and core curriculum lessons for K–12 math educators. Contact us to learn more!

What does a social, collaborative math classr...

In a social, collaborative classroom, math students find multiple ways to connect to each other, and to math. Find out how teachers and technology can work toge...

Learning mathematics through problem solving:...

Problem-based learning can put students on a path to math success. In this three-part series, you’ll learn what it is and how it looks in a classroom.

Sed posuere consectetur est at lobortis. Aenean eu leo quam. Pellentesque ornare sem lacinia quam venenatis vestibulum.

Routines for Mathematical Thinking & Engagement

Routines for mathematical thinking & engagement, by amy withers.

The beginning of the school year is filled with excitement and anticipation. There are materials to prepare and organize, lessons to plan, and classrooms to set up. As teachers, we think carefully about the norms, structures, and routines that we want to establish. Everything from housekeeping to how we communicate with each other to how we move about the classroom contribute to students feeling safe to share their thinking, take risks, and solve problems.

Thinking routines establish predictable patterns in ways of thinking and send strong messages about what is valued within the classroom community. Harvard’s Project Zero defines a thinking routine as “a set of questions or a brief sequence of steps used to scaffold and support student thinking.” In the context of mathematics, thinking routines can convey that it’s our thinking that matters, not just the answers. They can communicate that what is valued is our collective understanding, not our individual performance. Beginning a lesson with a thinking routine communicates that everyone has something to contribute, that our understanding is deepened through discourse; it is a way to ensure that every student experiences success. In contrast to a “mad minute” or other rote computational tasks that may start off a math class, the thinking routines we offer here focus on justification, flexible thinking, and clear communication.

Thinking routines are a great way to pique curiosity while being accessible to all students. Let’s take a look at a few examples of thinking routines you can use to start off your math class and set the tone for the rest of a lesson:

Notice and Wonder . This routine has become, well, quite routine in many classrooms! The power in notice and wonder lies in its accessibility to all students; all students can notice something and there are no incorrect responses to what we notice! Using visual images for a notice and wonder routine is a great way to further increase accessibility and to emphasize mathematical relationships over computation. Additionally, research supports the importance of visual mathematics for our learning. Education Development Center (EDC) has an extensive collection of images of different mobiles similar to the one below that can be used in a notice and wonder routine.

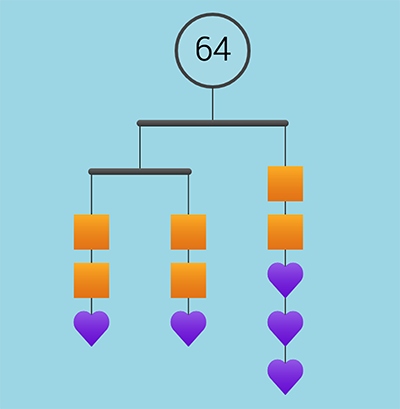
Looking at this image, what do you notice? What do you see? What does it make you wonder? What might your students see in this image, and what questions might they come up with?

Which One Doesn’t Belong? (Alternatively, Which One Is Unique?) . In this routine, there are, by design, several correct answers. Students are shown four quadrants with an image in each. Their job is to decide which of the four is different from the rest. Students can justify any of the four quadrants as being unique, and therefore the emphasis of the routine is on students’ reasoning. Many examples of and inspiration for images can be found on the site “Which One Doesn’t Belong?”

Look at the four triangles in this example. How is each one unique? What reasoning might your students use to prove how each is unique? What kinds of relationships and attributes would they focus on, and what kinds of conversations might develop from what they notice?

What’s the Same? What’s Different? In this routine, students are shown two side-by-side images and are tasked with sharing what they notice about how the images are the same or different. Again, the emphasis here is on justification and reasoning, and it gives students an opportunity to practice using precise language to describe the similarities and differences. Some inspiration for images can be found on Dr. Sue Looney’s site “Same but Different Math” . What might your young students say if presented with the following image?

True or False? This routine challenges students to evaluate whether or not an equation is true or false without evaluating each side! This is a way for students to focus on the relationships between numbers rather than on computational skills. For example, how could you decide if the following equation is true or false without evaluating each side? What mathematical relationships and big ideas are you using to decide?

659 + 357 = 660 + 356

When you use these or any other thinking routines to begin your math lesson, it’s important to consider what is accessible for all students as well as which big mathematical ideas you want your students to be thinking about that day. We want all students to experience success as they begin the lesson, and these routines allow for that while also engaging students in thinking about big ideas.

All students can and should experience success every day in the math classroom. This doesn’t mean that they won’t be challenged, make mistakes, or struggle. Starting class with a thinking routine is a way to ensure success while supporting students’ ability to reason, communicate their thinking, and develop confidence in mathematics. Thinking routines ensure that every student is successfully engaged in mathematical thinking from the beginning of the lesson. Success primes students to take on the mathematical challenges and intellectual risks of the day.

What other thinking routines have you used in your classroom? We encourage you to try these and other thinking routines and notice how they influence classroom culture and learning.

The contents of this blog post were developed under a grant from the Department of Education. However, those contents do not necessarily represent the policy of the Department of Education, and you should not assume endorsement by the Federal Government.

Math for All is a professional development program that brings general and special education teachers together to enhance their skills in planning and adapting mathematics lessons to ensure that all students achieve high-quality learning outcomes in mathematics.

Our Newsletter Provides Ideas for Making High-Quality Mathematics Instruction Accessible to All Students

Sign up for our newsletter, recent blogs.

• Social Justice in the Math Classroom May 30, 2024
• Parents and Teachers as Co-Constructors of Children’s Success as Mathematical Learners May 1, 2024
• The Problem with Word Problems March 11, 2024
• Honoring Diversity: What, why, and how? February 22, 2024
• Looking at a Student at Work January 3, 2024

Team & Partners

Testimonials

Newsletter Signup

Problem Solving in Mathematics

• Math Tutorials
• Pre Algebra & Algebra
• Exponential Decay
• Worksheets By Grade

The main reason for learning about math is to become a better problem solver in all aspects of life. Many problems are multistep and require some type of systematic approach. There are a couple of things you need to do when solving problems. Ask yourself exactly what type of information is being asked for: Is it one of addition, subtraction, multiplication , or division? Then determine all the information that is being given to you in the question.

Mathematician George Pólya’s book, “ How to Solve It: A New Aspect of Mathematical Method ,” written in 1957, is a great guide to have on hand. The ideas below, which provide you with general steps or strategies to solve math problems, are similar to those expressed in Pólya’s book and should help you untangle even the most complicated math problem.

Use Established Procedures

Learning how to solve problems in mathematics is knowing what to look for. Math problems often require established procedures and knowing what procedure to apply. To create procedures, you have to be familiar with the problem situation and be able to collect the appropriate information, identify a strategy or strategies, and use the strategy appropriately.

Problem-solving requires practice. When deciding on methods or procedures to use to solve problems, the first thing you will do is look for clues, which is one of the most important skills in solving problems in mathematics. If you begin to solve problems by looking for clue words, you will find that these words often indicate an operation.

Look for Clue Words

Think of yourself as a math detective. The first thing to do when you encounter a math problem is to look for clue words. This is one of the most important skills you can develop. If you begin to solve problems by looking for clue words, you will find that those words often indicate an operation.

Common clue words for addition  problems:

Common clue words for  subtraction  problems:

• How much more

Common clue words for multiplication problems:

Common clue words for division problems:

Although clue words will vary a bit from problem to problem, you'll soon learn to recognize which words mean what in order to perform the correct operation.

Read the Problem Carefully

This, of course, means looking for clue words as outlined in the previous section. Once you’ve identified your clue words, highlight or underline them. This will let you know what kind of problem you’re dealing with. Then do the following:

• Ask yourself if you've seen a problem similar to this one. If so, what is similar about it?
• What did you need to do in that instance?
• What facts are you given about this problem?
• What facts do you still need to find out about this problem?

Develop a Plan and Review Your Work

Based on what you discovered by reading the problem carefully and identifying similar problems you’ve encountered before, you can then:

• Define your problem-solving strategy or strategies. This might mean identifying patterns, using known formulas, using sketches, and even guessing and checking.
• If your strategy doesn't work, it may lead you to an ah-ha moment and to a strategy that does work.

If it seems like you’ve solved the problem, ask yourself the following:

• Does your solution seem probable?
• Does it answer the initial question?
• Did you answer using the language in the question?
• Did you answer using the same units?

If you feel confident that the answer is “yes” to all questions, consider your problem solved.

Tips and Hints

Some key questions to consider as you approach the problem may be:

• What are the keywords in the problem?
• Do I need a data visual, such as a diagram, list, table, chart, or graph?
• Is there a formula or equation that I'll need? If so, which one?
• Will I need to use a calculator? Is there a pattern I can use or follow?

Read the problem carefully, and decide on a method to solve the problem. Once you've finished working the problem, check your work and ensure that your answer makes sense and that you've used the same terms and or units in your answer.

• Examples of Problem Solving with 4 Block
• Using Percents - Calculating Commissions
• What to Know About Business Math
• Parentheses, Braces, and Brackets in Math
• How to Solve a System of Linear Equations
• How to Solve Proportions to Adjust a Recipe
• Calculate the Exact Number of Days
• What Is a Ratio? Definition and Examples
• Changing From Base 10 to Base 2
• Finding the Percent of Change Between Numbers
• Learn About Natural Numbers, Whole Numbers, and Integers
• How to Calculate Commissions Using Percents
• Overview of the Stem-and-Leaf Plot
• Understanding Place Value
• Probability and Chance
• Evaluating Functions With Graphs

Donate | Contact Us

NATIONAL CONTACT INFORMATION (317) 356-6284 FAX 317-356-6680 [email protected]

Our National Office is located at: 1412 Sadlier Circle East Drive Indianapolis, IN 46239 Get Directions

Pentathlon Institute

Active Problem-Solving

Learning to resolve problems that are continually undergoing change.

The Mathematics Pentathlon ® Program provides experiences in thought processes necessary for Active Problem Solving. The series of 20 Mathematics Pentathlon games provide K-7 students with experiences in deductive and inductive reasoning through the repeated use of sequential thought as well as nonlinear, intuitive thinking. Exposure to such forms of thought helps students relate to real-life problem-solving situations and learn to “think on their feet.”

The Four Sections below explain the following: Active Problem Solving Defined, What is Mathematics, Three Types of Mathematical Thought, and Conceptual Understanding Using Concrete and Pictorial Models.

Active-Problem Solving Defined

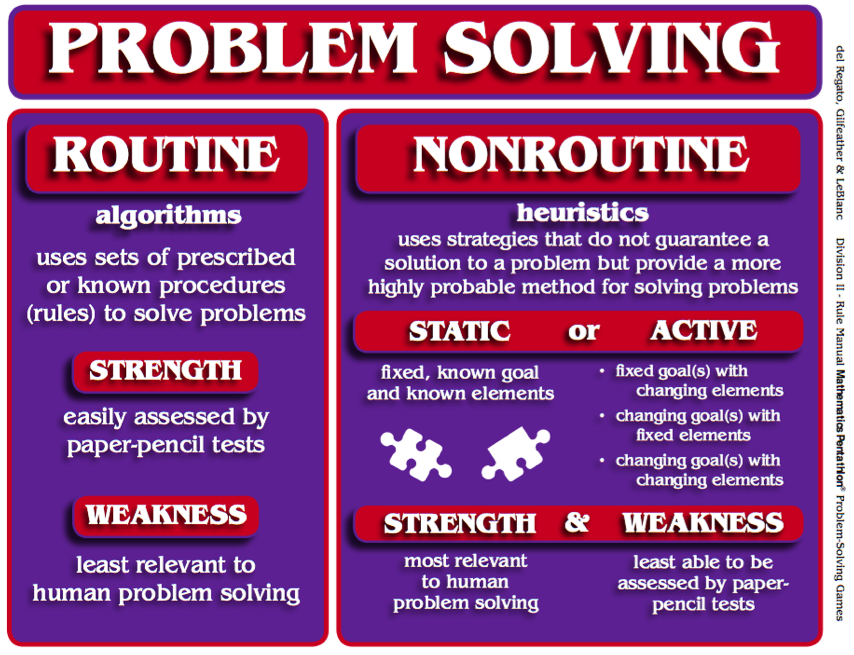
Problem solving can be divided into two categories:, routine & non-routine.

Routine Problem Solving , stresses the use of sets of known or prescribed procedures (algorithms) to solve problems. The strength of this approach is that it is easily assessed by paper-pencil tests. Since today’s computers and calculators can quickly and accurately perform the most complex arrangements of algorithms for multi-step routine problems, the typical workplace does not require a high level of proficiency in Routine Problem Solving. However, today’s workplace does require many employees to be proficient in Nonroutine Problem Solving.

Nonroutine Problem Solving , stresses the use of heuristics and often requires little to no use of algorithms. Unlike algorithms, heuristics are procedures or strategies that do not guarantee a solution to a problem but provide a more highly probable method for discovering a solution. Building a model and drawing a picture of a problem are two basic problem-solving heuristics. Studying end-of-game situations provides students with experiences in using the heuristics of reducing the problem to a similar but simpler problem and working a problem backwards, i.e. from its resolution to its initial state. Other heuristics include describing the problem situation, classifying information, and finding irrelevant information.

There Are Two Categories of Nonroutine Problem Solving:

Static and active.

Static-Nonroutine problems have a fixed, known goal and fixed, known elements that are used to resolve the problem. Solving a jigsaw puzzle is an example of a Static- Nonroutine problem. Given all pieces to a puzzle and a picture of the goal, learners are challenged to arrange the pieces to complete the picture. Various heuristics such as classifying the pieces by color, connecting the pieces that form the border, or connecting the pieces that form a salient feature to the puzzle, such as a flag pole, are typical ways in which people attempt to resolve such problems.

Active-Nonroutine problems may have a fixed goal with changing elements, a changing goal or alternative goals with fixed elements, or changing or alternative goals with changing elements. The heuristics used in this form of problem-solving are known as strategies. People who study such problems must learn to change or adapt their strategies as the problem unfolds.

What is Mathematics?

There is a growing belief in the mathematics community, as well as society in general, that the study of mathematics must develop in all students an understanding of mathematics that continues throughout one’s lifetime and evolves to meet ever-changing situations and variables. From our perspective, mathematics is an area of investigation that develops the ability to critically observe, classify, describe, and analyze data in a logical manner using both inductive and deductive methods. In contrast to the sterilized and unrelated manner in which school mathematics has often been taught, mathematics is a creative and aesthetic study of patterns and geometric and numerical relationships. It is dynamic rather than passive in nature and should involve students in strategic thinking by exploring multiple possibilities and variables that continually change, much like life.

The Mathematics Pentathlon® Program, which integrates Adventures in Problem Solving, Activity Books I & II, the Mathematics Pentathlon® Games and Investigation Exercises, Books I & II was designed to implement the definition of mathematics described above. The games are organized into four division levels by grade, K-1, 2-3, 4- 5, and 6-7 with five games at each level. The name of the Program, Mathematics Pentathlon®, was coined to liken it to a worldwide series of athletic events, the Decathlon component of the Olympics. In the world of athletics the Decathlon is appreciated for valuing and rewarding individuals who have developed a diverse range of athletic abilities. In contrast, the mathematics community as a whole has rarely valued or rewarded individuals with a diverse range of mathematics abilities. The Mathematics Pentathlon® Games promote diversity in mathematical thinking by integrating spatial/ geometric, arithmetic/computational, and logical/scientific reasoning at each division level. Since each of the 5 games requires students to broaden their thought processes, it attracts students from a wide range of ability levels, from those considered “gifted and talented” to “average” to “at-risk.”

The format of games was chosen for two reasons. First, games that are of a strategic nature require students to consider multiple options and formulate strategies based on expected countermoves from the other player. The Mathematics Pentathlon® further promotes this type of thought by organizing students into groups of four and teams of two. Teams alternate taking turns and team partners alternate making decisions about particular plays by discussing aloud the various options and possibilities. In this manner, all group members grow in their understanding of multiple options and strategies. As students play these games over the course of time, they learn to make a plan based on better available options as well as to reassess and adjust this plan based on what the other team acted upon to change their prior ideas. Through this interactive process of sharing ideas and possibilities, students learn to think many steps ahead, blending both inductive and deductive thinking. Second, games were chosen as a format since they are a powerful motivational tool that attracts students from a diverse range of abilities and interest levels to spend more time on task developing basic skills as well as problem-solving skills. While race-type games based on chance are commonly used in classrooms, they do not typically capture students’ curiosity for long periods of time. Students may play such games once or twice, but then lose interest since they are not seriously challenged. The Mathematics Pentathlon® Games have seriously challenged students to mature in their ability to think strategically and resolve problems that are continually undergoing change. As a result, we view active-problem solving and strategic thinking as described above as a critical focal point of the mathematics curriculum.

3 Types of Mathematical Thought

Integration of spatial/geometric, computational, and logical/scientific reasoning.

Most mathematics instruction stresses students’ knowledge of basic arithmetic facts. While the Mathematics Pentathlon Program provides a great deal of practice with mastery of the basic facts, it goes far beyond learning arithmetic skills. The Mathematics Content and Standards Chart for the 20 Mathematics Pentathlon Games shows how each game addresses several mathematical content and process objectives (see inside back cover of manual). These objectives have been clustered into logical/scientific reasoning, computational reasoning, and spatial/geometric reasoning. Each of these categories is described below.

Spatial/Geometric Reasoning

Spatial visualization involves the ability to image objects and pictures in the mind’s eye and to be able to mentally transform the positions and examine the properties of these objects/pictures. A large body of mathematics research concludes that spatial reasoning ability is highly related to higher-level mathematical problem-solving and geometric skills as well as students’ overall achievement in mathematics. Many of the Mathematics Pentathlon Games stress spatial reasoning and several integrate this form of thinking with logical and computational reasoning.

Computational Reasoning

Many of the Mathematics Pentathlon Games incorporate computation into the game structure. More time-on-task practicing arithmetic skills does indeed result in students’ increased performance in the classroom as well as on standardized tests. But in the Mathematics Pentathlon Games that stress computation, it is not sufficient to rely on arithmetic skills alone. To be successful in these games, students must also use their logical reasoning abilities to consider several options and to decide which ones will maximize their ability to reach the game’s goal(s).

Logical/Scientific Reasoning

One of the most important life skills, not to mention mathematical skills, is the ability to think logically. The process of observation, classification, hypothesizing, experimentation, and inductive and deductive thought are required for logical reasoning. Yet where do children learn these fundamental life skills? Strategic games provide students the opportunity to develop this form of thinking. Each of the Mathematics Pentathlon Games is a strategy game that develops students’ logical reasoning skills through the process of investigating a variety of options and choosing better options.  At the same time students develop scientific reasoning skills by learning how to be better observers of game-playing variables and options. Playing the games over the course of time allows for hypothetical reasoning to evolve since students analyze sequences of “if-then” situations and make choices based on linking inductive and deductive thought.

While each of the 20 games may stress one form of the mathematical thinking over another, each game integrates at least two categories of mathematical thinking. Furthermore, the five games at each Divisional level balance the three types of reasoning.

Conceptual Understanding Using Concrete and Pictorial Models Understanding

Since its inception, the National Council of Teachers of Mathematics (NCTM) has called for a conceptually-based curriculum in schools throughout the country. The most recent psychological and educational research has shown that conceptual understanding is a key attribute of individuals who are proficient in mathematics. Furthermore, a large body of research over the last four decades suggests that effective use of physical and pictorial models of mathematics concepts improves students’ conceptual understanding, problem-solving skills, and overall achievement in mathematics. Research also indicates that the use of concrete and pictorial models improves spatial visualization and geometric thinking.

The  Mathematics Pentathlon ®   Program  incorporates a variety of concrete and pictorial models to develop students’ conceptual understanding of many important mathematics concepts that involve computational, spatial, and logical reasoning. In addition, by playing these games in cooperative groups, as suggested in this publication, students also improve their oral and written communication skills through their discussion of mathematical ideas and relationships.

5 Steps to Teaching Students a Problem-Solving Routine

• Share article

By Jeff Heyck-Williams, the director of curriculum and instruction for Two Rivers Public Charter School

When I visited a 5th grade class recently, the students were tackling the following problem:

If there are nine people in a room and every person shakes hands exactly once with each of the other people, how many handshakes will there be? How can you prove your answer is correct using a model or numerical explanation?

There were students on the rug modeling people with Unifix cubes. There were kids at one table vigorously shaking each other’s hand. There were kids at another table writing out a diagram with numbers. At yet another table, students were working on creating a numeric expression. What was common across this class was that all of the students were productively grappling around the problem.

On a different day, I was out at recess with a group of kindergartners who got into an argument over a vigorous game of tag. Several kids were arguing about who should be “it.” Many of them insisted that they hadn’t been tagged. They all agreed that they had a problem. With the assistance of the teacher, they walked through a process of identifying what they knew about the problem and how best to solve it. They grappled with this very real problem to come to a solution that all could agree upon.

Then just last week, I had the pleasure of watching a culminating showcase of learning for our 8th graders. They presented to their families about their project exploring the role that genetics plays in our society. Tackling the problem of how we should or should not regulate gene research and editing in the human population, students explored both the history and scientific concerns about genetics and the ethics of gene editing. Each student developed arguments about how we as a country should proceed in the burgeoning field of human genetics, which they took to Capitol Hill to share with legislators. Through the process, students read complex text to build their knowledge, identified the underlying issues and questions, and developed unique solutions to this very real problem.

Problem-solving is at the heart of each of these scenarios and is an essential set of skills our students need to develop. They need the abilities to think critically and solve challenging problems without a roadmap to solutions. At Two Rivers Public Charter School in the District of Columbia, we have found that one of the most powerful ways to build these skills in students is through the use of a common set of steps for problem-solving. These steps, when used regularly, become a flexible cognitive routine for students to apply to problems across the curriculum and their lives.

The Problem-Solving Routine

At Two Rivers, we use a fairly simple routine for problem-solving that has five basic steps. The power of this structure is that it becomes a routine that students are able to use regularly across multiple contexts. The first three steps are implemented before problem-solving. Students use one step during problem-solving. Finally, they finish with a reflective step after problem-solving.

Problem Solving from Two Rivers Public Charter School on Vimeo .

Before Problem-Solving: The KWI

The three steps before problem-solving: We call them the K-W-I.

The “K” stands for “know” and requires students to identify what they already know about a problem. The goal in this step of the routine is two-fold. First, the student needs to analyze the problem and identify what is happening within the context of the problem. For example, in the math problem above, students identify that they know there are nine people and each person must shake hands with each other person. Second, the student needs to activate their background knowledge about that context or other similar problems. In the case of the handshake problem, students may recognize that this seems like a situation in which they will need to add or multiply.

The “W” stands for “what” a student needs to find out to solve the problem. At this point in the routine, the student always must identify the core question that is being asked in a problem or task. However, it may also include other questions that help a student access and understand a problem more deeply. For example, in addition to identifying that they need to determine how many handshakes in the math problem, students may also identify that they need to determine how many handshakes each individual person has or how to organize their work to make sure that they count the handshakes correctly.

The “I” stands for “ideas” and refers to ideas that a student brings to the table to solve a problem effectively. In this portion of the routine, students list the strategies that they will use to solve a problem. In the example from the math class, this step involved all of the different ways that students tackled the problem from Unifix cubes to creating mathematical expressions.

This KWI routine before problem-solving sets students up to actively engage in solving problems by ensuring they understand the problem and have some ideas about where to start in solving the problem. Two remaining steps are equally important during and after problem-solving.

During Problem-Solving: The Metacognitive Moment

The step that occurs during problem-solving is a metacognitive moment. We ask students to deliberately pause in their problem-solving and answer the following questions: “Is the path I’m on to solve the problem working?” and “What might I do to either stay on a productive path or readjust my approach to get on a productive path?” At this point in the process, students may hear from other students that have had a breakthrough or they may go back to their KWI to determine if they need to reconsider what they know about the problem. By naming explicitly to students that part of problem-solving is monitoring our thinking and process, we help them become more thoughtful problem-solvers.

After Problem-Solving: Evaluating Solutions

As a final step, after students solve the problem, they evaluate both their solutions and the process that they used to arrive at those solutions. They look back to determine if their solution accurately solved the problem, and when time permits, they also consider if their path to a solution was efficient and how it compares with other students’ solutions.

The power of teaching students to use this routine is that they develop a habit of mind to analyze and tackle problems wherever they find them. This empowers students to be the problem-solvers that we know they can become.

The opinions expressed in Next Gen Learning in Action are strictly those of the author(s) and do not reflect the opinions or endorsement of Editorial Projects in Education, or any of its publications.

Sign Up for The Savvy Principal

Problem Solving Activities: 7 Strategies

• Critical Thinking

Problem solving can be a daunting aspect of effective mathematics teaching, but it does not have to be! In this post, I share seven strategic ways to integrate problem solving into your everyday math program.

In the middle of our problem solving lesson, my district math coordinator stopped by for a surprise walkthrough. 

I was so excited!

We were in the middle of what I thought was the most brilliant math lesson– teaching my students how to solve problem solving tasks using specific problem solving strategies. 

It was a proud moment for me!

Each week, I presented a new problem solving strategy and the students completed problems that emphasized the strategy. 

Genius right? 

After observing my class, my district coordinator pulled me aside to chat. I was excited to talk to her about my brilliant plan, but she told me I should provide the tasks and let my students come up with ways to solve the problems. Then, as students shared their work, I could revoice the student’s strategies and give them an official name. 

What a crushing blow! Just when I thought I did something special, I find out I did it all wrong. 

I took some time to consider her advice. Once I acknowledged she was right, I was able to make BIG changes to the way I taught problem solving in the classroom. 

When I Finally Saw the Light

To give my students an opportunity to engage in more authentic problem solving which would lead them to use a larger variety of problem solving strategies, I decided to vary the activities and the way I approached problem solving with my students. 

Problem Solving Activities

Here are seven ways to strategically reinforce problem solving skills in your classroom. 

Seasonal Problem Solving

Many teachers use word problems as problem solving tasks. Instead, try engaging your students with non-routine tasks that look like word problems but require more than the use of addition, subtraction, multiplication, and division to complete. Seasonal problem solving tasks and daily challenges are a perfect way to celebrate the season and have a little fun too!

Cooperative Problem Solving Tasks

Go cooperative! If you’ve got a few extra minutes, have students work on problem solving tasks in small groups. After working through the task, students create a poster to help explain their solution process and then post their poster around the classroom. Students then complete a gallery walk of the posters in the classroom and provide feedback via sticky notes or during a math talk session.

Notice and Wonder

Before beginning a problem solving task, such as a seasonal problem solving task, conduct a Notice and Wonder session. To do this, ask students what they notice about the problem. Then, ask them what they wonder about the problem. This will give students an opportunity to highlight the unique characteristics and conditions of the problem as they try to make sense of it. 

Want a better experience? Remove the stimulus, or question, and allow students to wonder about the problem. Try it! You’ll gain some great insight into how your students think about a problem.

Math Starters

Start your math block with a math starter, critical thinking activities designed to get your students thinking about math and provide opportunities to “sneak” in grade-level content and skills in a fun and engaging way. These tasks are quick, designed to take no more than five minutes, and provide a great way to turn-on your students’ brains. Read more about math starters here ! 

Create your own puzzle box! The puzzle box is a set of puzzles and math challenges I use as fast finisher tasks for my students when they finish an assignment or need an extra challenge. The box can be a file box, file crate, or even a wall chart. It includes a variety of activities so all students can find a challenge that suits their interests and ability level.

Calculators

Use calculators! For some reason, this tool is not one many students get to use frequently; however, it’s important students have a chance to practice using it in the classroom. After all, almost everyone has access to a calculator on their cell phones. There are also some standardized tests that allow students to use them, so it’s important for us to practice using calculators in the classroom. Plus, calculators can be fun learning tools all by themselves!

Three-Act Math Tasks

Use a three-act math task to engage students with a content-focused, real-world problem! These math tasks were created with math modeling in mind– students are presented with a scenario and then given clues and hints to help them solve the problem. There are several sites where you can find these awesome math tasks, including Dan Meyer’s Three-Act Math Tasks and Graham Fletcher’s 3-Acts Lessons . 

Getting the Most from Each of the Problem Solving Activities

When students participate in problem solving activities, it is important to ask guiding, not leading, questions. This provides students with the support necessary to move forward in their thinking and it provides teachers with a more in-depth understanding of student thinking. Selecting an initial question and then analyzing a student’s response tells teachers where to go next. 

Ready to jump in? Grab a free set of problem solving challenges like the ones pictured using the form below. 

Which of the problem solving activities will you try first? Respond in the comments below.

Shametria Routt Banks

• Assessment Tools
• Content and Standards
• Differentiation
• Math & Literature
• Math & Technology
• Math Routines
• Math Stations
• Virtual Learning
• Writing in Math

You may also like...

2 Responses

This is a very cool site. I hope it takes off and is well received by teachers. I work in mathematical problem solving and help prepare pre-service teachers in mathematics.

Thank you, Scott! Best wishes to you and your pre-service teachers this year!

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

©2024 The Routty Math Teacher.   All Rights Reserved.  Designed by Ashley Hughes.

Privacy overview, grade level.

Mathematical Mysteries

Revealing the mysteries of mathematics

How to Solve Math Problems: Non-Routine Problems

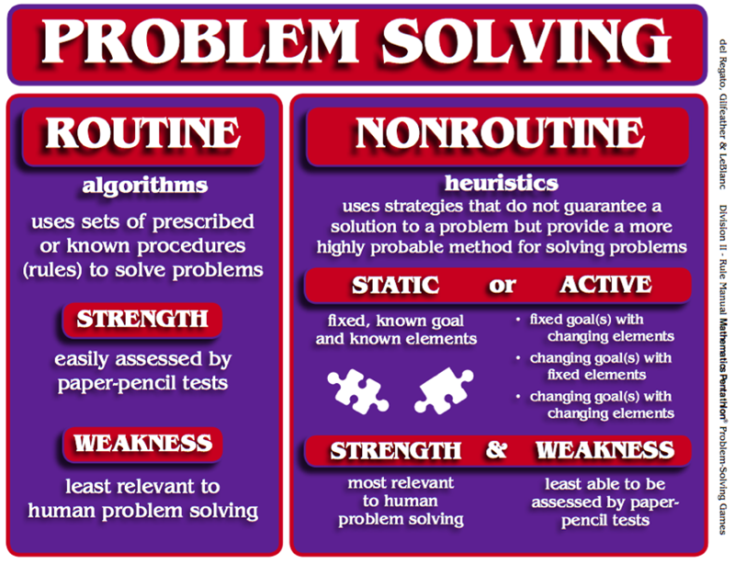
Nonroutine Problem Solving , stresses the use of heuristics [3] and often requires little to no use of algorithms. Unlike algorithms, heuristics are procedures or strategies that do not guarantee a solution to a problem but provide a more highly probable method for discovering a solution. Building a model and drawing a picture of a problem are two basic problem-solving heuristics. Studying end-of-game situations provides students with experiences in using the heuristics of reducing the problem to a similar but simpler problem and working a problem backwards, i.e. from its resolution to its initial state. Other heuristics include describing the problem situation, classifying information, and finding irrelevant information. [1]

There Are Two Categories of Nonroutine Problem Solving: Static and Active

Static-Nonroutine  problems have a fixed, known goal and fixed, known elements that are used to resolve the problem. Solving a jigsaw puzzle is an example of a Static- Nonroutine problem. Given all pieces to a puzzle and a picture of the goal, learners are challenged to arrange the pieces to complete the picture. Various heuristics such as classifying the pieces by color, connecting the pieces that form the border, or connecting the pieces that form a salient feature to the puzzle, such as a flag pole, are typical ways in which people attempt to resolve such problems. [1]

Active-Nonroutine  problems may have a fixed goal with changing elements, a changing goal or alternative goals with fixed elements, or changing or alternative goals with changing elements. The heuristics used in this form of problem-solving are known as strategies. People who study such problems must learn to change or adapt their strategies as the problem unfolds. [1]

What is non-routine problem-solving in math?

A non-routine problem is any complex problem that requires some degree of creativity or originality to solve. Non-routine problems typically do not have an immediately apparent strategy for solving them. Often times, these problems can be solved in multiple ways.

Incorporating non-routine problem solving into your math program is one of the most impactful steps you can take as an educator. By consistently allowing your students to grapple with these challenging problems, you are helping them acquire essential problem-solving skills and the confidence needed to successfully execute them. [2]

Step 1: Understand

This is a time to just think! Allow yourself some time to get to know the problem. Read and reread. No pencil or paper necessary for this step. Remember, you cannot solve a problem until you know what the problem is!

• Does the problem give me enough information (or too much information)?
• What question is being asked of me?
• What do I know and what do I need to find out?
• What should my solution look like?
• What type of mathematics might be required?
• Can I restate the problem in my own words?
• Are there any terms or words that I am unfamiliar with?

Step 2: Plan

Now it’s time to decide on a plan of action! Choose a reasonable problem-solving strategy. Several are listed below. You may only need to use one strategy or a combination of strategies.

• Draw a picture or diagram
• Make an organized list
• Make a table
• Solve a simpler related problem
• Find a pattern
• Guess and check
• Act out a problem
• Work backward
• Write an equation
• Use manipulatives
• Break it into parts
• Use logical reasoning

Step 3: Execute

Alright! You understand the problem. You have a plan to solve the problem. Now it’s time to dig in and get to work! As you work, you may need to revise your plan. That’s okay! Your plan is not set in stone and can change anytime you see fit.

• Am I checking each step of my plan as I work?
• Am I keeping an accurate record of my work?
• Am I keeping my work organized so that I could explain my thinking to others?
• Am I going in the right direction? Is my plan working?
• Do I need to go back to Step 2 and find a new plan?
• Do I think I have the correct solution? If so, it’s time to move on to the next step!

Step 4: Review

You’ve come so far, but you’re not finished just yet! A mathematician must always go back and check his/her work. Reviewing your work is just as important as the first 3 steps! Before asking yourself the questions below, reread the problem and review all your work.

• Is my answer reasonable?
• Can I use estimation to check if my answer is reasonable?
• Is there another way to solve this problem?
• Can this problem be extended? Can I make a change to this problem to create a new one?
• I didn’t get the correct answer. What went wrong? Where did I make a mistake?

[1] “Pentathlon Institute Active Problem-Solving”. 2023.  mathpentath.org . https://www.mathpentath.org/active-problem-solving/ .

[2] Tallman, Melissa. 2015. “Problem Solving In Math • Teacher Thrive”. Teacher Thrive. https://teacherthrive.com/non-routine-problem-solving/ .

[3] A heuristic is  a mental shortcut commonly used to simplify problems and avoid cognitive overload .

Additional Reading

“101 Great Higher-Order Thinking Questions for Math”. 2023.  elementaryassessments.com . https://elementaryassessments.com/higher-order-thinking-questions-for-math/ .

⭐ “Developing Mathematics Thinking with HOTS (Higher Order Thinking Skills) Questions”. 2023. saydel.k12.ia.us . https://www.saydel.k12.ia.us/cms_files/resources/Developing%20Mathematics%20Thinking%20with%20HOTS%20Questions%20(from%20classroom%20observations)PDF.pdf .

“Higher Order Thinking Skills in Maths”. 2017.  education.gov.Scot . https://education.gov.scot/resources/higher-order-thinking-skills-in-maths/ .

“How to Increase Higher Order Thinking”. 2023.  Reading Rockets . https://www.readingrockets.org/topics/comprehension/articles/how-increase-higher-order-thinking .

⭐ I suggest that you read the entire reference. Other references can be read in their entirety but I leave that up to you.

Website Powered by WordPress.com .

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Published 2016 Revised 2019

Mathematical Problem Solving in the Early Years: Developing Opportunities, Strategies and Confidence

• familiar contexts
• meaningful purposes
• mathematical complexity.

• which they understand - in familiar contexts,
• where the outcomes matter to them - even if imaginary,
• where they have control of the process,
• involving mathematics with which they are confident.
• taking some from one doll and giving to another, in several moves,
• starting again and dealing, either in ones or twos,
• taking two from each original doll and giving to the new doll,
• collecting the biscuits and crumbling them into a heap, then sharing out handfuls of crumbs.

• brute force: trying to hammer bits so that they fit,
• local correction: adjusting one part, often creating a different problem,
• dismantling: starting all over again,
• holistic review: considering multiple relations or simultaneous adjustments e.g. repairing by insertion and reversal.
• getting a feel for the problem, looking at it holistically, checking they have understood e.g. talking it through or asking questions;
• planning, preparing and predicting outcomes e.g. gathering blocks together before building;
• monitoring progress towards the goal e.g. checking that the bears will fit the houses;
• being systematic, trying possibilities methodically without repetition, rather than at random, e.g. separating shapes tried from those not tried in a puzzle;
• trying alternative approaches and evaluating strategies e.g. trying different positions for shapes;
• refining and improving solutions e.g. solving a puzzle again in fewer moves (Gifford, 2005: 153).
• Getting to grips:     What are we trying to do?    
• Connecting to previous experience:  Have we done anything like this before?
• Planning:      What do we need?
• Considering alternative methods:   Is there another way?
• Monitoring progress:    How does it look so far?
• Evaluating solutions:    Does it work?  How can we check?  Could we make it even better?

• Construction - finding shapes which fit together or balance
• Pattern-making - creating a rule to create a repeating pattern
• Shape pictures - selecting shapes with properties to represent something
• Puzzles - finding ways of fitting shapes to fit a puzzle
• Role-play areas - working out how much to pay in a shop
• Measuring tools - finding out how different kinds of scales work
• Nesting, posting, ordering - especially if they are not obvious
• Robots - e.g. beebots: directing and making routes
• preparing, getting the right number e.g. scissors, paper for creative activities
• sharing equal amounts e.g. at snack time
• tidying up, checking nothing is lost
• gardening and cooking  e.g. working out how many bulbs to plant where, measuring amounts in a recipe using scales or jugs
• games, developing rules, variations and scoring
• PE: organising in groups, timing and recording

• Decision making - what shall we call the new guinea pig?
• Parties, picnics and trips e.g. how much lemonade shall we make?
• Design Projects - the role play area, new outdoor gardens or circuits
• Hiding games - feely bags with shapes, the 'Box' game
• Story problems - e.g. unfair sharing, with remainders and fractions, making things to fit giants or fairies

Math Language Routines: Discourse with a Purpose

By Dr. Kristen Taylor, IM Certified® Facilitator 

Math teachers can talk all day about math! We get super excited when we encounter someone else who enjoys these conversations as well.

But too many of our students don’t get to experience that joyful discourse, which limits their understanding of and positive experiences with math.

How would our students’ math learning and perception about math improve if they also had regular opportunities to talk about math? How might these opportunities help us create a world where learners know, use, and enjoy mathematics?

Let’s explore the Math Language Routines, which are embedded in IM K–12 Math.

What are math language routines?

Stanford Graduate School of Education’s Understanding Language and the Stanford Center for Assessment, Learning, and Equity (SCALE) designed eight Math Language Routines (MLRs) to help teachers “amplify, assess, and develop students’ language” in math class. These routines are structured, but adaptable to the content and classroom context. The routines “emphasize the use of language that is meaningful and purposeful, not inauthentic or simply answer-based . . . [and] can and should be used to support all students learning mathematics.” (from Understanding Language/SCALE’s Principles for the Design of Mathematics Curricula: Promoting Language and Content Development ) There are four specific design principles used to entice students to discuss the concepts and ensure that the discussions provide opportunities for students to learn something new. The Math Language Routines also provide opportunities for students to engage in the Common Core’s Standards for Mathematical Practice .

As students engage in math language routines, MLRs help students to advance their thinking in the following ways:  

• OPTIMIZING OUTPUT as students describe their own math thinking to others orally and visually or writing as physical, graphical, pictorial, or symbolic representations.
• SUPPORT SENSE-MAKING as students scaffold their thinking and amplify language so students can make their own meaning between concepts and representations.
• CULTIVATE CONVERSATION by providing opportunities to simultaneously make meaning, communicate that meaning, and refine the way content understandings are communicated.
• MAXIMIZE META-AWARENESS as students organize their own experiences, ideas, and learning for themselves through reflection of the experience of discussing their math ideas, reasoning, and language.

This doesn’t just mean that teachers tell students to talk about math and they do. We know that if we simply open the space and tell students to talk, much of the discussion will veer off-topic. Math Language Routines help teachers create a structure in which students can bring those four design principles to life.

Let’s see what opportunities each MLR provides for students to practice exploring their math thinking and the MLRs’ connections to the Standards for Mathematical Practice .

MLR 1: Stronger and Clearer Each Time – Students write a response to a math problem, then verbally share their response with a partner to get feedback from the listener to improve the response, and revise their original written response based on the feedback they received.

Students learn to both listen to their own thoughts and the thoughts of another with the purpose of strengthening their “first draft” thinking. This MLR strengthens student communication of their thinking. They make their explanations clearer through repeated “reviews” and revisions, which allow them to practice giving, receiving, and applying constructive feedback, and develop listening skills. This MLR helps students communicate their mathematical reasoning with greater clarity and focus.

(This connects to Standards for Mathematical Practice 1: Make sense of problems and persevere in solving them, 3: Construct viable arguments and critique the reasoning of others, and 6: Attend to precision.

As students verbalize and review in writing the strategies they used and justification of those strategies, students have the opportunity to get feedback which can be used to critique the precision of their solution strategy and answer.)

MLR 2: Collect and Display – Students access their own and others mathematical ideas as the teacher scribes the language, strategies, and concepts students use during partner, small group, or whole-class discussions using written words, diagrams, and pictures.

By creating stable representations of student thoughts, the teacher extends the involvement of students in the math classroom. Student contributions are displayed for everyone to see. During that discussion as well as future conversations, students refer to these written ideas to improve the clarity and focus of their own communication. They can use the vocabulary, reference previous relationships between concepts, and identify new connections. This MLR helps make student thinking visible and promotes student ownership over mathematical ideas.

(Standards for Mathematical Practice 3: Construct viable arguments and critique the reasoning of others, and 6: Attend to precision.

As students view the thinking of their classmates from the representation, they can address any differences they see between their representation and their classmates’ representation in type and kind, further pushing students to find the most efficient or precise representation to solve the problem.)

MLR 3: Critique, Correct, and Clarify – Students rewrite a math response from an example that is incorrect, incomplete, or otherwise ambiguous.

In addition to providing students with a space to further engage in math, students employ a “growth mindset” and consider revisions to their work in order to strengthen their communication. This MLR helps students “try on” others’ math thinking in order to improve it.

(Standards for Mathematical Practice 3: Construct viable arguments and critique the reasoning of others.

Similar to doing error analysis, students have the opportunity to engage with a strategy for solving that might be different from theirs in order to find ways to improve the situation representation, address and clarify misconceptions about the math, and “borrow” parts of the strategy that were relevant to add to their toolbox.)

MLR 4: Information Gap – In a group, each student has different parts of the math context and they work together to piece together that information orally and/or visually to bridge the gap between the parameters of a math situation and a question to solve a math problem.

As students work to make sense of individual pieces of information about a math context, they also identify what information they need in order to answer the math question. This creates an environment where students work together as they consider which strategies are the most efficient and what information they need to know to solve the problem. This MLR helps students explore math contexts with a purpose.

(Standards for Mathematical Practice 2: Reason abstractly and quantitatively, and 4: Model with mathematics.

As students imagine the kinds of information they need to know and explain why they need to know that information, they are building an understanding of the problem and possible solutions related to the parameters of the problem and the kinds of data they need to solve for an answer.)

MLR 5: Co-Craft Questions and Problems – Students take a provided math “answer” to create a problem that could result in that answer or use a given context to create a problem that can be answered using that context.

With this MLR, students use their creativity to explore a math context as they iterate their understanding in order to identify questions that can be asked and answered by the context. As students share their understandings with others, they also uncover the importance of slowing down to explore and think before they try to answer a question, which results in students understanding the math more deeply. This MLR helps students define math contexts.

(Standards for Mathematical Practice 4: Model with mathematics.

By creating their own questions and problems, students learn to visualize the parameters of the problem as they consider what kind of answers are possible with the information the problem provides.)

MLR 6: Three Reads – Students are guided to read the problem three separate times with three separate purposes with quick discussions between each read.

When students slow down to consider how they can use the information in a problem, they notice things about their understanding of the problem context and their own math understanding that they wouldn’t have noticed before. Giving students a purpose to read helps to focus students to identify (1) the context of the mathematical situation, (2) relationships that exist within that context, and (3) strategies that can be used to answer the question using the problem context. This MLR helps students think metacognitively about their math problem solving.

(Standards for Mathematical Practice 1: Make sense of problems and persevere in solving them.

As students set a purpose for reading each of the three times, students practice and see the importance of understanding the problem context and using the information they know from the problem in order to identify a strategy for solving that relates directly to the problem context and available information.)

MLR 7: Compare and Connect – Students identify, compare, and contrast their own understandings with other students’ mathematical approaches, representations, concepts, examples, and language.

As students encounter other’s math thinking, this MLR opens the floor for students to consider how they see and talk about math. This MLR specifically helps students interact with each other’s thinking.

(Standards for Mathematical Practice 4: Model with mathematics, 6: Attend to precision, and 7: Look for and make use of structure.

As students compare (find differences) and connect (find similarities) between their strategy for solving and another classmate’s strategy for solving, students mine their understanding of the math concept in relation to the structure and steps of another student’s understanding of the math. This allows both students to attend to precision because to be understood by another, they have to be precise with their explanation.)

MLR 8: Discussion Supports – Students access strategies in multi-modal ways, like visuals, aural, animation/movement, and symbols as modes, to help students better make sense of complex language, ideas, and classroom communication.

Enhancing access to the mathematical context through these multi-modal supports helps students develop understanding while also continuing to work on their mathematical communication. This MLR helps students deepen their mathematical understandings, and find ways to communicate their understandings in different ways.

(Standards for Mathematical Practice 1: Make sense of problems and persevere in solving them, 3: Construct viable arguments and critique the reasoning of others, 5: Use appropriate tools strategically, and 6: Attend to precision.

Using discussion supports helps students to see the reasoning of others as well as identify which tools to solve are most appropriate. In using these supports, students can be successful with in-depth or multistep problems with support from teachers and classmates.)

Consider what your students need to encounter math more deeply and in collaboration with others. More heads are better than one!

Looking for more support for distance learning ? Check out IM’s collection of resources.

to the IM Blog and Newsletter

RECENT POSTS

• Annotate and Acknowledge August 9, 2024
• Getting Ready for 2024–2025 Back to School with Illustrative Mathematics August 1, 2024
• Getting Started with Illustrative Mathematics July 11, 2024
• Math Successes Multiply with a Growth Mindset June 13, 2024
• Visualizing IM K-5 Math in Specialized Academic Settings: Part 3 May 31, 2024
• Back to School (5)
• Grades 3–5 (109)
• Grades 6–8 (120)
• Grades 9–12 (96)
• Grades K–2 (90)
• Grades K–5 (56)
• Partners (4)
• Professional Learning (77)
• Recent Blog Posts (8)
• Uncategorized (3)

Popular Tags

Improving Students’ Problem-Solving Flexibility in Non-routine Mathematics

• Conference paper
• First Online: 30 June 2020
• Cite this conference paper

• Huy A. Nguyen   ORCID: orcid.org/0000-0002-1227-6173 13 ,
• Yuqing Guo 13 ,
• John Stamper 13 &
• Bruce M. McLaren 13  

Part of the book series: Lecture Notes in Computer Science ((LNAI,volume 12164))

Included in the following conference series:

• International Conference on Artificial Intelligence in Education

6392 Accesses

1 Citations

A key issue in mathematics education is supporting students in developing general problem-solving skills that can be applied to novel, non-routine situations. However, typical mathematics instruction in the U.S. too often is dominated by rote learning, without exposing students to the underlying reasoning or alternate ways to solve problems. As a first step in addressing this problem, we present a cognitive task analysis study that investigates how students without a mathematics-related background solve novel non-routine problems. We found that most students were able to identify the underlying pattern that yields the final solution in each problem. Furthermore, they tended to use various forms of visualization in their draft work, but occasionally made computational mistakes. Based on these results, we propose our plan for developing an instructional platform that leverages learning science principles to train students in problem-solving abilities.

You have full access to this open access chapter,  Download conference paper PDF

We’re sorry, something doesn't seem to be working properly.

Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

• Problem-solving flexibility
• Non-routine mathematics

1 Introduction

The ability to tackle non-routine problems – those that cannot be solved with a known method or formula and require analysis and synthesis as well as creativity [ 9 ] – is becoming increasingly important in the 21st century [ 5 ]. However, when faced with a non-routine problem, U.S. students tend to apply memorized procedures incorrectly rather than modify them or develop new solutions [ 8 ]. One possible source for this difficulty is the typical instructional focus in U.S. schools on memorization and application of routine procedures [ 2 , 6 , 7 ]. Such an approach makes students proficient at executing rote procedures, but it does little to help them understand the conceptual basis for the procedures or to think creatively about novel problems - both of which are essential for developing problem-solving flexibility.

An important first step in addressing this issue is to assess how students currently approach non-routine problem solving, so that we can design the appropriate learning interventions. In this work, we present an empirical cognitive task analysis where participants were asked to think aloud while solving a series of non-routine problems from discrete mathematics. We chose this domain because discrete math problems can often be tackled from multiple perspectives while not requiring any advanced background beyond the high school curriculum [ 3 ]. Based on the findings from this study, we propose our plan for developing a tutoring system for non-routine problem-solving ability. Then, we discuss the system’s broader implications and the challenges we need to address in deploying this system at scale.

2 Assessing Students’ Problem-Solving Skills

We conducted interview sessions with three students at a private university in a midwest US city. None of the students had a mathematics-related background. The participants were asked to solve three non-routine mathematics problems on paper in one hour. They were also encouraged to think aloud and write down their draft work. The three problems in our study, taken from [ 3 ], and a brief summary of their sample solutions, are as follows.

In an air show there are twenty rows. The first row contains one seat, the second three seats, the third five seats, the fourth seventh seats, and so on. How many seats are there in total ?

Sample solution: In the first row there is 1 seat. In the first two rows there are 1 + 3 =  4 seats. In the first three rows there are 1 + 3 + 5 =  9 seats. In the first four rows there are 1 + 3 + 5 + 7 =  16 seats. In the first five rows there are 1 + 3 + 5 + 7 + 9 =  25 seats. Based on this pattern, in the first k rows there are k 2 seats. In our case, there are 20 rows and therefore 400 seats in total.

Find all integers between 1 and 99 (inclusive) with all distinct digits.

Sample solution: there are 99 integers between 1 and 99 in total, and 9 of them have non-distinct digits, namely 11, 22, 33, …, 88, 99. Hence, the remaining 90 integers have distinct digits.

What is the digit in the ones place of 2 57 ?

Sample solution: Looking at the sequence of powers of 2–2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, … – we see that the corresponding sequence of digits in the ones places is 2, 4, 8, 6, 2, 4, 8, 6, 2, 4, … In other words, this sequence is a cycle of length 4. Therefore the last digit of 2 57 is that of 2 53 , which is that of 2 49 , …, which is that of 2 1 , which is 2.

We then analyzed recordings of the participants’ think-aloud and their draftwork, from which we derived the following insights:

Pattern Identification.

Participants were aware that they had to find a pattern or formula to solve the problems, because it was not feasible to directly compute the final answer. All participants were able to identify the expected pattern for each problem as outlined above, except for one student who failed to do so for Problem 1 . While this participant realized that the number of seats on row k is the k-th positive odd number, this pattern alone was insufficient to solve the problem.

Visualization.

Participants tended to visualize the problem by drawing examples and making lists or tables (Fig.  1 ). They expressed that these visualizations were crucial in helping them identify the correct pattern and solve the problem.

Participants’ attempts at visualizing the problem in their draftworks.

Computation.

Participants occasionally made computational mistakes while calculating the initial sequence values, especially in Problem 3 . As a consequence, they could not identify any pattern based on the wrong values, and took some time to realize the mistake. All students who corrected their mistakes were able to subsequently solve the problem.

In summary, we found that participants were aware of the idea behind identifying patterns, and they all did so via some kind of visualization. On the other hand, computational mistakes, while not directly related to our learning objectives, can be detrimental to the overall problem-solving process. From these insights, we propose the following next steps.

3 Developing a Tutoring System for Flexible Problem-Solving

Moving forward, our plan is to iteratively conduct more cognitive task analysis interviews and develop a prototype of the system. Our initial conceptualization of how the system will work is as follows. A single round of exercise in the system incorporates four learning stages, all of which are built on established learning principles: 1) Reviewing a worked example of a non-routine mathematics problem, 2) Explaining the worked example to a partner, 3) Solving a new problem which is isomorphic to the worked example problem, and 4) Explaining the isomorphic solution to a partner. Between rounds, the student can review previous solutions, look at materials related to the problem space, or practice basic math skills. This design is intended to (1) formally introduce students to a complete solution through worked examples, (2) reinforce their understanding of the worked example through self-explanation, and (3) assess students’ learning through an isomorphic problem. Our hypothesis is that through the learning system, students will get a better sense of how to approach a novel non-routine problem, so that in case they have not yet found the solution – for example, like the participant in our study who did not identify the true pattern in Problem 1 – they can still adopt a different viewpoint and explore other strategies.

We have already begun mapping the problem space by developing a non-routine problem-solving flowchart and identifying sets of potential non-routine problem solutions. Once we have tested our solution space, we will develop and pilot a low fidelity paper prototype version of the system with college students to further refine the mathematical content and identify areas for revision to the design. We are also looking at which technological features could be useful for students learning in this domain. As a first step, our system will include a canvas for students to perform their draftwork on, as well as a simple calculator interface with basic arithmetic operations to help students avoid computational mistakes. An important follow-up question is whether students’ draftwork can be analyzed to infer their thinking process, which could in turn guide the design of appropriate feedback mechanics. While this task has previously been performed manually by domain experts [ 1 ], employing a machine learning technique to automate it to some extent would greatly enhance the system’s adaptive support functionality and scalability.

4 Conclusion

This research will provide concrete, generalizable evidence about the utility and implementation of worked examples, multiple solutions, and self-explanation to promote skills in non-routine problem solving. Results will inform future tutoring system design by identifying how and when the instructional features are most beneficial for developing problem-solving skills. We also intend to have a practical impact by distributing a tutoring system that is accessible to a wide range of students, including lower-performing students who would typically not be exposed to these types of problems and strategies [ 1 , 4 ]. In addition, we will provide a teacher’s guide to support educators in using the system adaptively to support their instructional goals.

Arslan, C., Yazgan, Y.: Common and flexible use of mathematical non routine problem solving strategies. Am. J. Educ. Res. 3 , 1519–1523 (2015)

Google Scholar  

Crooks, N.M., Alibali, M.W.: Defining and measuring conceptual knowledge in mathematics. Dev. Rev. 34 , 344–377 (2014)

Article   Google Scholar  

Johnson, K., Herr, T.: Problem Solving Strategies: Crossing the River with Dogs: and Other Mathematical Adventures. Key Curriculum Press, New York (2001)

Kolovou, A., Van Den Heuvel-Panhuizen, M., Bakker, A.: Non-routine problem solving tasks in primary school mathematics textbooks–a needle in a haystack. Math. Prob. Solving Primary School 8 , 45 (2011)

Neubert, J.C., Mainert, J., Kretzschmar, A., Greiff, S.: The assessment of 21st century skills in industrial and organizational psychology: complex and collaborative problem solving. Ind. Organ. Psychol. 8 , 238–268 (2015)

Richland, L.E., Stigler, J.W., Holyoak, K.J.: Teaching the conceptual structure of mathematics. Educ. Psychol. 47 , 189–203 (2012)

Stigler, J., Hiebert, J.: Understanding and improving classroom mathematics instruction: an overview of the TIMSS video study. In: ACER National Conference 1997, pp. 52–65 (1997)

Stigler, J.W., Givvin, K.B., Thompson, B.J.: What community college developmental mathematics students understand about mathematics. MathAMATYC Educ. 1 , 4–16 (2010)

Woodward, J., et al.: Improving Mathematical Problem Solving in Grades 4 through 8. IES Practice Guide. NCEE 2012-4055. What Works Clearinghouse (2012)

Download references

Author information

Authors and affiliations.

Carnegie Mellon University, Pittsburgh, PA, 15213, USA

Huy A. Nguyen, Yuqing Guo, John Stamper & Bruce M. McLaren

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Huy A. Nguyen .

Editor information

Editors and affiliations.

Federal University of Alagoas, Maceió, Brazil

Ig Ibert Bittencourt

University College London, London, UK

Mutlu Cukurova

Carleton University, Ottawa, ON, Canada

Kasia Muldner

Rose Luckin

University of Malaga, Málaga, Spain

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Switzerland AG

About this paper

Cite this paper.

Nguyen, H.A., Guo, Y., Stamper, J., McLaren, B.M. (2020). Improving Students’ Problem-Solving Flexibility in Non-routine Mathematics. In: Bittencourt, I., Cukurova, M., Muldner, K., Luckin, R., Millán, E. (eds) Artificial Intelligence in Education. AIED 2020. Lecture Notes in Computer Science(), vol 12164. Springer, Cham. https://doi.org/10.1007/978-3-030-52240-7_74

Download citation

DOI : https://doi.org/10.1007/978-3-030-52240-7_74

Published : 30 June 2020

Publisher Name : Springer, Cham

Print ISBN : 978-3-030-52239-1

Online ISBN : 978-3-030-52240-7

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Problem Solving in Math

  What is non-routine problem-solving in math?

A non-routine problem is any complex problem that requires some degree of creativity or originality to solve.  Non-routine problems typically do not have an immediately apparent strategy for solving them.  Often times, these problems can be solved in multiple ways.

Incorporating non-routine problem solving into your math program is one of the most impactful steps you can take as an educator. By consistently allowing your students to grapple with these challenging problems, you are helping them acquire essential problem-solving skills and the confidence needed to successfully execute them.

One of the best ways to prepare students for solving non-routine problems is by familiarizing them with the four steps of problem-solving. I have a set of questions and/or guides for each step, that students can use to engage in an inner-dialogue as they progress through the steps.  You can download this free Steps to Non-Routine Problem Solving Flip-Book {HERE}.

1. Understand: 

This is a time to just think! Allow yourself some time to get to know the problem.  Read and reread. No pencil or paper necessary for this step.  Remember, you cannot solve a problem until you know what the problem is!

• Does the problem give me enough information (or too much information)?
• What question is being asked of me?
• What do I know and what do I need to find out?
• What should my solution look like?
• What type of mathematics might be required?
• Can I restate the problem in my own words?
• Are there any terms or words that I am unfamiliar with?

Now it’s time to decide on a plan of action! Choose a reasonable problem-solving strategy. Several are listed below.  You may only need to use one strategy or a combination of strategies.

• draw a picture or diagram
• make an organized list
• make a table
• solve a simpler related problem
• find a pattern
• guess and check
• act out a problem
• work backward
• write an equation
• use manipulatives
• break it into parts
• use logical reasoning

3. Execute: 

Alright! You understand the problem.  You have a plan to solve the problem.  Now it’s time to dig in and get to work! As you work, you may need to revise your plan. That’s okay! Your plan is not set in stone and can change anytime you see fit.

• Am I checking each step of my plan as I work?
• Am I keeping an accurate record of my work?
• Am I keeping my work organized so that I could explain my thinking to others?
• Am I going in the right direction? Is my plan working?
• Do I need to go back to Step 2 and find a new plan?
• Do I think I have the correct solution? If so, it’s time to move on to the next step!

4. Review: 

You’ve come so far, but you’re not finished just yet!  A mathematician must always go back and check his/her work. Reviewing your work is just as important as the first 3 steps! Before asking yourself the questions below, reread the problem and review all your work.

• Is my answer reasonable?
• Can I use estimation to check if my answer is reasonable?
• Is there another way to solve this problem?
• Can this problem be extended? Can I make a change to this problem to create a new one?
• I didn’t get the correct answer.  What went wrong? Where did I make a mistake?

My Brain Power Math resources are the perfect compliment to this free flip-book.  Each book has a collection of non-routine math problems in a variety of formats.

• Depth and Complexity
• End of the School Year
• Reading Comprehension
• Reading Fluency
• Uncategorized

LATEST ON INSTAGRAM

Sinta Score

• Other Journals

This journal is indexed by:

• For Readers
• For Authors
• For Librarians

Additional Menu

View My Stats

• Announcements
• CITEDNESS IN SCOPUS

Mathematical Problem-Solving Behaviors of the Routine Solver

The research refined the theories of students’ characteristics in solving mathematical problems and constructed a holistic understanding of their problem-solving behaviors. It aimed at describing the problem-solving behaviors of a routine problem solver. The routine bridged the gap between the expert and the novice. This research used a qualitative approach which was carried out in six stages. The research participant was Rina (female, pseudonym), one of the 11th-grade students from one of the high schools in Palangka Raya City, Central Kalimantan, Indonesia. The selection of the participant was based on certain criteria. The instruments were three mathematics problems and semi-structured interviews. The trustworthiness of the research was fulfilled through credibility, dependability, and transferability checking. The results showed that the routine could understand problems and was able to identify the known and the target. The routine only focused on developing a plan which was based on a lack of concepts, limited previous experiences, or limited strategies. Problem-solving behaviors of the routine were between the expert and the novice.

Ary, D., Jacobs, L. C., & Sorensen, C. (2006). Introduction to Research in Education (8th ed.). Wadsworth.

Bahar, A., & Maker, C. J. (2015). Cognitive backgrounds of Problem Solving: A comparison of open ended vs. closed mathematics problems. Eurasia Journal of Mathematics, Science and Technology Education, 11(6), 1531-1546. 10.12973/eurasia.2015.1410a.

Bloomberg, L. D., & Volpe, M. (2008). Completing your qualitative dissertation: A roadmap from beginning to end. Sage Publications, Inc.

Botia, M. L., & Orozo, L. H. (2009). Crtitical review of problem solvng process traditional theoritical models. International Journal of Psychological Research, 2(1), 62-72.

Cadez, H. T., & Kolar, M. D. (2015). Comparison of types of generalizatons and problem-solving schemas used to solve a mathematical problems. Educational Studies in Mathematics, 89, 283-306.

Carlson, M. P., & Bloom, I. (2005). The cyclic nature of problem solving: an emergent multidimensional problem solving framework. Educational Studies in Mathematics, 58, 45-75. 10.1007/s10649-005-0808-x.

Goldstein, E. B. (2011). Cognitive psychology:Connecting mind, research, and everyday experience (3th ed.). Wadsworth.

Gruwel, S. B., Wopereis, I., & Vermetten, Y. (2015). Information problem solving by experts and novices: Analysis of a complex cognitive skill. Computer in Human Behaviour, 21(3), 487-508. doi: 10.1016/j.chb.2004.10.005.

Khasanah, V. N., Usodo, B., & Subanti, S. (2018). Student's thinking process in solving word problems in geometry. Journal pf Physics: Conference Series, 1-6. 10.1088/1742-6596/1013/1/012133.

Lodico, M. G., Spaulding, D. T., & Voegtle, K. H. (2006). Method in educational research: From theory to practice. John Willey & Sons, Inc.

Mairing, J. P. (2018). Pemecahan masalah matematika: Cara siswa memperoleh jalan untuk berpikir kreatif dan sikap positif [Mathematics problem solving: How students acquire creative thinking and positive attitudes]. Alfabeta.

Mairing, J. P. (2017). Thinking process of naive problem solvers to solve mathematical problems. International Educational Studies, 10(1), 1-10. 10.5539/ies.v10n1p1.

Mairing, J. P., Budayasa, I. K., & Juniati, D. (2012). Perbedaan profil pemecahan masalah peraih medali OSN matematika berdasarkan jenis kelamin. Jurnal Ilmu Pendidikan, 18(2), 125–134. 10.17977/jip.v18i2.3612.

Mairing, J. P., Budayasa, I. K., & Juniati, D. (2011). Profil pemecahan masalah peraih medali OSN. Jurnal Pendidikan dan Pembelajaran, 18(1), 65–71.

Muir, T., Beswick, K., & Williamson, J. (2008). I am not very good at solving problems: An exploration of student’s problem solving behaviours. The Journal of Mathematical Behaviour, 27(3), 228–241.

National Council of Teachers of Mathematics [NCTM]. (2000). Principles and standards for school mathematics. The National Council of Teachers of Mathematics, Inc.

Pape, S. J. (2004). Middle school children’s problem solving behavior: A cognitive analysis from a reading comprehension perspective. Journal for Research in Mathematics Education, 35 (3), 187-219. 10.2307/30034912.

Polya, G. (1973). How to solve it (2 ed.). Princeton University Press.

Posamenteir, A. S., & Krulik, S. (2009). Problem solving in mathematics grades 3–6, powerful strategies to deepen understanding. Corwin A SAGE Company.

Pretz, J. E., Naples, A. J., & Sternberg, R. J. (2003). Recognizing, defining, and representing problems. In T. P. Solving, The psychology of problem solving (pp. 3-30). Cambridge University Press.

Reiss, K., & Torner, G. (2007). Problem solving in the mathematics classroom: The German perspective. ZDM Mathematics Education, 39, 431-441.

Sanjaya, A., Johar, R., Ikhsan, M., & Khairi, L. (2018). Students' thinking process in solving mathematical problems based on the levels of mathematical ability. Journal of Physics: Conference Series, 1-7. 10.1088/1742-6596/1088/1/012116.

Setiawani, S., Fatahillah, A., Dafik, Oktavianingthyas, E., & Wardani, D. Y. (2019). The students' creative thinking process in solving mathematics problem based on wallas' stages. IOP Conference Series: Earth and Environmental Science.243, pp. 1-8. IOP Publishing Ltd. 10.1088/1755-1315/243/1/012052.

Singer, F. M., & Voica, C. (2013). A problem-solving conceptual framework and its implications in designing problem posing tasks. Educational Studies in Mathematics, 83 (1), 9-18.

Sternberg, R. J., & Sternberg, K. (2012). Cognitive psychology (6 ed.). Wadsworth Cengage Learning.

Strauss, A., & Corbin, J. (1998). Basics of qualitative research, tehniques and procedures for developing grounded theory. SAGE Publications, Inc.

• There are currently no refbacks.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

Problem Solving Heuristics on Non-Routine Problems of College Students

In the K-12 curriculum, problem solving and critical thinking skills have been the center of the framework for Mathematics curriculum in order to develop lifelong learners. With this, problem solving in Mathematics is highly valued. This descriptive comparative study determined the level of problem solving heuristics on non-routine problems of college freshmen at Mindoro State College of Agriculture and Technology. Employing a self-structured problem solving test composed of five non-routine problems, result showed that most of the students were classified as apprentice in heuristics knowledge which means that the skills and strategies used in general have focus but with limited clarity. In procedural knowledge, most of the students were also classified as apprentice which means that generally, most of the students made partial use of appropriate procedures and were not precise in using mathematical terms, principles and procedures. In conceptual knowledge, most of the students were also classified as apprentice which means that the students can extract the essence of the problem but most of them were unable to use this information to solve the problem properly. However, problem solving skills of college students did not differ in terms of heuristics, procedural and conceptual knowledge. Furthermore, the study showed that the most commonly used heuristics are making a model or diagram, using a formula, eliminating, and considering a simpler case. Relevant to this, the study recommended that Mathematics faculty should develop effective measures to enhance problem solving skills of the students such as integration of heuristics in teaching Mathematics problem solving and more exposure to non-routine problems.

Related Papers

Denis A Tan

Numerous researches from abroad had been investigating the mathematical problem solving process among students, but little is done with regards to the mathematical problem solving heuristics among high school students in the Philippines. This paper is a portion of a grounded theory research conducted by the researcher. This article presents the portion in which case study design was utilized to find out the mathematical problem solving heuristics among Filipino high school students. Thirty participants representing different problem solving skills ranging from poor to good problem solvers were interviewed over a period of three months. Interviews were analyzed and mathematical problem solving heuristics were identified. Filipino senior high school students utilized the following heuristics when they solved mathematical problems: use of logic or common sense, look for a clue, use an equation, draw a picture, solve or recall similar or equivalent problem, make a list, find a pattern, and make a table, make a diagram, use of mathematical expressions, use a model and use a representation. Other solution strategies used by the participants in the study were trial-and-error, guessing, guess-and-test, skip counting, use of the basic operations, use of adding techniques and recall and create formula. Participants in the study used the solution strategies as stand-alone or a combination of two or more strategies.

Journal on Efficiency and Responsibility in Education and Science

Melanie Gurat

Jiřina Ondrušová

The paper describes one of the ways of developing pupils’ creative approach to problem solving. The described experiment is a part of a longitudinal research focusing on improvement of culture of problem solving by pupils. It deals with solving of problems using the following heuristic strategies: Analogy, Guess – check – revise, Systematic experimentation, Problem reformulation, Solution drawing, Way back and Use of graphs of functions. Most attention is paid to the question whether short-term work, in this case only over the period of three months, can result in improvement of pupils’ abilities to solve problems whose solving algorithms are easily accessible. It also answers the question which strategies pupils will prefer and with what results. The experiment shows that even short-term work can bear positive results as far as pupils’ approach to problem solving is concerned.

PEOPLE: International Journal of Social Sciences

Attakan Vongyai

List of Figures 3 List of Tables 5 Introduction 7 Overview 7 Background 8 The Mathematical Problem Solving Suite of Studies 8 Literature Review 9 Mathematics Problem Solving 9 Metacognition and Problem Solving 11 Mathematical tasks as developed by the teachers 14 Methodology 15 Design of the Study 15 Explanation of changes in work program due to shifts in Principal Investigators ...... 17 Data collection 18 Data analysis approach 21 Findings 25 Overall findings 25 The Teachers‘ Classroom Practices 31 Student Pair Work 44 Student Problem Solving Exercises 67 Discussion 83 Pedagogical implications 83 Limitations of the current study 91 Conclusions and Further Research 92 Acknowledgement 94 References 95 Appendices 101 Appendix 1: Information for participants 102 Appendix 2: Coding Scheme Manual 105 Appendix 3: Pair work exercise 115 Appendix 4: An Adapted Artzt & Armour-Thomas Cognitive-Metacognitive Framework 117 Appendix 5: Problem solving exercise – Pretest 120 FINAL RESEARCH REPOR...

Universal Journal of Educational Research

Horizon Research Publishing(HRPUB) Kevin Nelson

Descriptive design was utilized to identify the problem-solving heuristics and mathematical abilities of students in solving non-routine problems in terms of conceptual understanding, procedural knowledge, and problem-solving skill. Both quantitative and qualitative data were gathered from students' mathematical solutions, journals, and interviews. Six non-routine problems were given to thirty Grade 10 students. Each level of mathematical achievement includes ten students who were randomly selected using their averages in the first two quarters. "Compute or Simplify" and "Model or Diagram" were the usual strategies employed by the Proficient respondents. On the other hand, Compute or Simplify is the most frequent strategy used by Apprentice Problem Solvers. The first strategy includes straightforward application of rules in mathematics, correctly sequencing the operations and using other mathematical procedures, while the second includes the use of concrete representations and figures, acting out and formulation of algebraic statements. All the strategies were considered in solving the six non-routine problems. Most students under the three levels solved the problem by combining two or more strategies in getting the answer. Three students who belong to above-average mathematical achievement are considered proficient problem solvers while twenty-seven students who belong to average and below average are regarded as Apprentice Problem Solvers. No student among the thirty was considered Novice. Students performed best in conceptual understanding and least in problem-solving skills. The results revealed that there are no significant differences in the levels of each of the three components of mathematical abilities of students when they are grouped according to mathematical achievement.

Al-Jabar: Jurnal Pendidikan Matematika

Munaya Nikma Rosyada

Problem solving is an essential aspect of students' mathematical activities. This ability could practice by using heuristic strategies in learning. Besides, these are assured to be able to promote metacognitive skills. In the implementation, teachers faced several challenges. This research aims to describe the challenges of teachers in implementing learning with heuristic strategies. This research is a descriptive qualitative. Participants of this research were 12 junior high school mathematics teachers from 12 high schools in the Special Region of Yogyakarta and Central Java. Data collection was taken by questionnaire and added with documentation. Data were analyzed using the Miles & Huberman stage-data reduction, data display, and drawing conclusion/verification. The data then validated using triangulation technique. The results revealed that some of teacher has already implement heuristic strategy in the learning process, but unable to define the heuristic strategy correctly. In its implementation, teachers experience several obstacles. These obstacles were found in providing nonroutine problems to students, solving problems by students, and in discussions conducted to solve problems.

International Electronic Journal of Mathematics Education

Phebby Teoh

seçil saygılı

The main purpose of this study was to investigate how well certain students in a high school solve non-routine problems. These problem situation required the use of their conceptual understanding of mathematics and their procedural knowledge of the algorithm involved in the solution. Results of analysis of students’ solutions showed that each student employed at least three problem solving strategies. Nine out of the ten possible problem solving strategies were used at least once to solve the eight non-routine problems. The most frequently used strategies were making systematic list, looking for patterns, logical reasoning and making a model or diagram. Those who performed well were also proficient in the use of solution strategies.

Online International Interdisciplinary Research Journal

Satinder Dhillon

The present investigation was undertaken with an aim to study the effectiveness of Polya’s heuristic approach to problem solving in acquisition of mathematical concepts among secondary school students.. For this purpose 320 secondary school students from Moga district of Punjab state were taken as a sample. The tool used was Mathematical Concept Acquisition Test (MCAT) on selected topics of Mathematics of class IX (developed by the investigator). Instructional material (Modules) based on Problem Solving Instructional Strategy on selected topics of Mathematics for Class IX was also prepared by the investigator. It was validated by the subject experts and later on was implemented to the experimental group. The present study employed an experimental method with “pre-test post-test”design. Results showed that students taught through problem solving instructional strategy were found to achieve significantly high on the acquisition of mathematical concepts than taught through traditional teaching method.

Loading Preview

Sorry, preview is currently unavailable. You can download the paper by clicking the button above.

RELATED PAPERS

John Hedberg

Mathematics Education Research Journal

Jarmila Novotna

International Group for the Psychology of Mathematics Education

Azita Manouchehri

Procedia Social and Behavioral Sciences

Pimpaka Intaros

sciepub.com SciEP

Petr Eisenmann

Journal on Efficiency and Responsibility in Education and Science, 11(3), 53-64

Journal Research Paper

International Journal of Education and Practice

Ruby Thomas

AJHSSR Journal

Nita Delima

Benjamin Rott

Carlo Magno

Encyclopedia of Mathematics Education

Manuel Santos-Trigo

Education Quarterly Reviews

Nurdan Ozrecberoglu

IJRISE Journal

Alipato a Journal of Basic Education

Rene Belecina

Belgin Bal İncebacak

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

• The Big Think Interview
• Your Brain on Money
• Explore the Library
• The Universe. A History.
• The Progress Issue
• A Brief History Of Quantum Mechanics
• 6 Flaws In Our Understanding Of The Universe
• Michio Kaku
• Neil deGrasse Tyson
• Michelle Thaller
• Steven Pinker
• Ray Kurzweil
• Cornel West
• Helen Fisher
• Smart Skills
• High Culture
• The Present
• Hard Science
• Special Issues
• Starts With A Bang
• Everyday Philosophy
• The Learning Curve
• The Long Game
• Perception Box
• Strange Maps
• Free Newsletters
• Memberships

The big myth that keeps people from loving math

• There is no secret code or single method to solve a mathematical problem.
• This “answer-getting” myth leads to disempowerment when learning math.
• To counteract the myth, don’t focus on the answer but the process.

Teaching math as if there’s only one correct way to solve a problem makes us think that we’re problem-solving, but instead, we’re “answer-getting.” I’ve seen it so many times, but none bothers me more than watching elementary and middle school students solve word problems in this way.

Consider this typical middle school prompt: A store is selling 6 bags of marbles for $18. What is the unit price for a bag of marbles? When I read this problem, I picture a child looking up at me and asking, “Does ‘of’ mean multiplication?” It has happened to me so many times when I visit math classrooms.

There’s no secret code. Of could mean “multiply,” but it might not. These are the highly counterproductive questions that children ask when they have been presented with a “single way” to solve word problems, such as looking for keywords. 

In this example, the students may immediately multiply 6 × 18. If you then ask them why the unit price of a single bag of marbles would cost $108 — and be so much more than the price of 6 bags of marbles — they will look at you with uncertainty. This is the end result of answer-getting.

Problem-solving is a distinct cognitive experience. Instead, we ask, what is happening in the problem? It is not mindlessly following a single prescriptive set of steps. The way to solve this problem, and every problem, is to understand what is happening. But that means there will be many paths to the answer. How I understand the problem might be quite unlike how you understand it.

The right way is the wrong way

When we are taught to rely on a singular, step-by-step process as the true way to solve a math problem, we turn off our problem-solving brain. These skills require continuous work to keep them sharp, and the constant reliance on someone else’s “exact right” method dulls them. Over the years, we may even lose at least some of our problem-solving acumen by not using it.

This reliance also discourages courage — we need to take chances to solve problems, and insistence on following a singular method prevents us from risking wrong answers via experimentation.

We can solve problems in many distinct ways. In fact, trying different approaches is fun as well as instructive, and it is necessary when problem-solving gets hard — which is often when the problems are most worth solving. Engineers who write software code or build bridges make a conscious attempt to solve problems in more than one way, even when a solution is readily available to them. 

Why not solve it and move on?

First of all, if you dig deeper to find more than one solution, you can decide which one among them is less expensive, more durable, or more elegant — whichever outcome matters most to you. Second, and perhaps more significant, when problem-solving gets really hard and the way ahead isn’t clear, you need to be ready to try anything. And the first step of the “try anything” approach is to back up and examine a problem from every angle, or at least from more angles than you initially see.

In the real world, of course, we often resort to looking at problems from fresh angles out of desperation. “Try anything” is the motto. As one member of a two-working-parents household with elementary school twins during the COVID-19 pandemic, we often were compelled to try anything to solve problems regarding work, social distancing protocols, on-and-off remote school, and limited childcare.

To expose the myth of a single correct method for the sham that it is, we need to understand the consequences of answer-getting versus problem-solving. Because we’ve been brainwashed into believing that answer-getting is good and because most of us spent years in answer-getting math curricula, we don’t realize the negative effects it has on us.

Here are typical ways we respond in an answer-getting environment:

• The mind goes blank. For a moment, nothing occurs to us because we’re not allowed to use our minds creatively.
• Racing heart. We react anxiously as we try to remember how the teacher did the math on the board. What was her first step again?
• Negative self-talk. For a moment, we have the germ of an idea, an instinct about how to start solving a challenging math problem, but because we’ve been conditioned to seek the answer only one way, we chastise ourselves for thinking we know better than what we’ve been taught, and we revert to standard operating procedure.
• Reluctance to talk through questions and concerns. We’re embarrassed to bring up these issues with others, assuming they are “right way” adherents. This reluctance to involve others is an obstacle to a creative, collaborative process.

The overarching effect of an answer-getting system is disempowerment. We feel defeated before even attempting to work on a problem.

Here are recent conversations I have had with children and adults on what this sort of math feels like:

“I want to use decimals. The teacher wants me to use fractions for no reason. I just have to do what he says. There is no freedom to do the math the way you want to do it, even if my way is easier for me. No one listens to me.”

“I actually remember getting dinged on a high school math test even when I had the right answer, but I had solved it my own way. As a teenager, that made me furious. Now looking back as an adult, I think about it like tennis. If you are drilling me so I learn or improve a new skill like backhand volleys, then I can understand the reasoning for forcing a specific approach. But if you have no reason whatsoever for forcing your way on me, it still steams me to think about it.”

A problem-solving approach conjures significantly contrasting responses — responses that reflect a sense of empowerment and courage. Ideally, schools would teach math with problem-solving as its driving principle rather than the myth of a single right way. To approach this ideal, however, we need to understand what problem-solving is all about.

Math should be taught as a collaborative process, much as other subjects are taught.

How to counteract the myth

We make math a performative rather than a learning experience. When the teacher asks the class, “What is the answer to 63 plus 37?” he turns math into an individual sport.

Add the myth of speed, and each student is scrambling to come up with the answer first and win the game. The answer becomes the only thing that matters, and both understanding and collaboration fall by the wayside.

No doubt, some of you might wonder if I’ve lost my math mind. After all, we need to get the answers right so that we can purchase the right amount of carpeting to cover a room’s floor or make sure that our rocket makes it to the moon. 

Again, this is an issue of integrative complexity. Of course, we need to know what 63 + 37 equals. But if that’s all we know, then we’re missing out on a lot of what math offers.

Fortunately, we can learn in a way that we obtain precision as well as other benefits. Consider again 63 + 37. What if the teacher framed the question this way: “Don’t tell me the answer. It’s 100. How would you start calculating 63 plus 37 in your head? What is your first step?” Now math is a process.

I have gotten the chance to hear second graders’ brains working at this moment many times. Each time is a joy. One might say, “I broke this up as 60 plus 30 plus 3 plus 7. And the next thing in my head I saw was that it was 93 plus 7. And then I knew that was 100.” Another second grader might offer another option: “I looked at this for a moment, and I saw that 3 and 7 make 10. So I knew I had a 60 plus 30 plus 10. And I know that’s 100.”

This is the math people need in their lives. This is what is needed to build bridges. It’s also how you build a deep math sense. 

Math should be taught as a collaborative process, much as other subjects are taught. We often view math as distinct from other subjects in K–8, as something that must be taught as an individual sport where everyone is on his or her own to come up with the right answer first. Other subjects are taught as team sports, ones where process matters, where students don’t rely on tricks, where students are encouraged to work together, and where a variety of ways to answer may be acceptable. But when it comes to math, collaboration and process work are subordinated or eliminated.

Homework Q&A

Drag image here or click to upload

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

Math AI Solver

Use our AI math solver to solve any math homework problem online for free

Tackle Your Math Homework with Our AI Math Solver

Struggling to do your math homework? HIX Tutor’s AI Math Solver simplifies math problems. Get fast, accurate math solutions in one click with our state-of-the-art math AI solver.

Why Use HIX Tutor’s Math AI Homework Solver

Comprehensive support.

Math AI Solver can assist with math at all grade levels, ranging from elementary math to university and beyond.

Step-by-Step Solutions

Get detailed explanations for each step of the problem to gain a better understanding of your math homework.

24/7 Availability

Access our AI math solver anytime to meet your homework needs around the clock to ensure that you never miss a deadline.

Save Time and Money

Get answers to math problems in record time and save on the cost of math tutors with our free math AI solver tool.

Technologically Advanced

We offer the latest in AI math technology to ensure accurate answers to any math problems including algebra, geometry, calculus, etc.

Streamlined Learning

Our AI math problem solvers make learning all kinds of math easier by providing step-by-step guidance and answers.

Experience the Best Math AI Solver on the Market

Stuck on a difficult math question? Math AI Solver is here to assist you:

Submit Your Math Query

Type in your math question or upload the document or an image of the homework problem.

Let Math AI Solver Do Its Magic

Wait just a few moments while our advanced math homework AI tool analyzes the question and prepares an accurate solution.

Receive the Correct Answer

Receive a detailed, step-by-step solution to your math query that includes an accurate answer.

Other AI Homework Helpers

Demystify topics ranging from basic mechanics to advanced electromagnetism with detailed solutions

Chemistry AI

HIX Tutor's AI chemistry homework helper is your go-to companion to master chemistry problem-solving.

Clarify doubts, and get insights on complex processes and terminologies. Get accurate answers to hard.

HIX Tutor’s AI Math Problem Solver Features at a Glance

✅ Accurate AI solutions	Eliminate the risk of errors and mistakes
📝 Rapid homework response	Get correct answers in just moments
📚 Comprehensive math support	Covers maths at all grade levels
📈 Ultimate math tutor	Boost your maths grade and school success

1. What is Math AI?

A Math AI is an artificial intelligence-powered tool designed to solve complex mathematical problems efficiently and accurately. By utilizing advanced algorithms and computational power, Math AI can provide step-by-step solutions, offer insights into problem-solving strategies, and enhance our overall understanding of various mathematical concepts.

2. What math subjects does the AI math problem solver cover?

Our AI math solver tool is trained to solve a wide range of math subjects, including but not limited to, algebra, geometry, calculus, trigonometry, calculus, and more.

3. How long does this math AI take to get an answer to my math question?

HIX Tutor's math AI Solver is available 24/7 and delivers correct, step-by-step solutions to maths questions almost immediately after you submit the query.

4. What's the best Math AI solver?

HIX Tutor is the best Math AI that offers comprehensive solutions for solving complex mathematical problems. With its advanced features, such as step-by-step explanations, personalized learning paths, and interactive problem-solving tools, HIX Tutor aims to help students and professionals better understand mathematical concepts and improve their problem-solving skills.

5. How does HIX Tutor's AI for maths work?

HIX Tutor's math AI helper utilizes advanced algorithms and deep learning techniques to analyze and understand math problems. It breaks down the problem into steps, applies relevant mathematical concepts, and provides detailed explanations for each step of the solution.

6. Is HIX Tutor's mathematics AI solver accurate?

Yes, our math AI solving tool is designed to deliver accurate solutions. It has been trained on a vast dataset of mathematical problems to ensure its proficiency in providing reliable answers. However, it's important to note that while our tool strives for accuracy, occasional errors or misunderstandings may occur.

7. Is HIX Tutor's math AI solver replace the need for a maths tutor?

While our maths AI tool is designed to provide comprehensive support and step-by-step solutions, it is not intended to replace the guidance and expertise of a human maths tutor. It can be a valuable tool to supplement your learning and provide quick answers, but for in-depth understanding and tailored guidance, a maths tutor may still be beneficial in certain situations.

8. Is this math AI free to use?

Yes, you can try Math AI Solver at no cost. Once you’ve reached your free question limit, you’ll need to purchase an affordable subscription.

Discover Frequently Asked Math Questions and Their Answers

• How do you write the quadratic function #y=x^2+14x+11# in vertex form?
• How many points does #y=-2x^2+x-3# have in common with the vertex and where is the vertex in relation to the x axis?
• How do you solve #4x^4 - 16x^2 + 15 = 0#?
• How do you solve #2x^2+3x-2=0#?
• How do you solve #7(x-4)^2-2=54# using any method?
• How do you solve #x^2 + 5x + 6 = 0# algebraically?
• How do you use factoring to solve this equation #3x^2/4=27#?
• What is the vertex of # y = (1/8)(x – 5)^2 - 3#?
• How do you solve #| x^2+3x-2 | =2#?
• How do you solve #2x²+3x=5 # using the quadratic formula?
• How do you find the derivative of #y=tan(3x)# ?
• How do you differentiate #f(x)= 1/ (lnx)# using the quotient rule?
• How do you differentiate #(3+sin(x))/(3x+cos(x))#?
• What is the derivative of this function #sin^-1(x/4)#?
• What is the derivative of this function #y=sin^-1(2x)#?
• What is the derivative of this function #arcsec(x^3)#?
• What is the derivative of #y=sin(tan2x)#?
• How do you differentiate #cos(pi*x^2)#?
• What is the derivative of #f(x)=(x^2-4)ln(x^3/3-4x)#?
• What is the derivative of #y=3sin(x) - sin(3x)#?
• A triangle has corners at #(5 ,1 )#, #(2 ,9 )#, and #(4 ,3 )#. What is the area of the triangle's circumscribed circle?
• How can we find the area of irregular shapes?
• A triangle has vertices A, B, and C. Vertex A has an angle of #pi/2 #, vertex B has an angle of #( pi)/3 #, and the triangle's area is #24 #. What is the area of the triangle's incircle?
• An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from #(7 ,1 )# to #(8 ,5 )# and the triangle's area is #27 #, what are the possible coordinates of the triangle's third corner?
• A triangle has corners at #(7 , 9 )#, #(3 ,7 )#, and #(4 ,8 )#. What is the radius of the triangle's inscribed circle?
• Circle A has a center at #(2 ,3 )# and a radius of #1 #. Circle B has a center at #(0 ,-2 )# and a radius of #4 #. Do the circles overlap? If not, what is the smallest distance between them?
• A parallelogram has sides A, B, C, and D. Sides A and B have a length of #2 # and sides C and D have a length of # 7 #. If the angle between sides A and C is #pi/4 #, what is the area of the parallelogram?
• What is a quadrilateral that is not a parallelogram and not a trapezoid?
• Your teacher made 8 triangles he need help to identify what type triangles they are. Help him?: 1) #12, 16, 20# 2) #15, 17, 22# 3) #6, 16, 26# 4) #12, 12, 15# 5) #5,12,13# 6) #7,24,25# 7) #8,15,17# 8) #9,40,41#
• A triangle has corners A, B, and C located at #(3 ,5 )#, #(2 ,9 )#, and #(4 , 8 )#, respectively. What are the endpoints and length of the altitude going through corner C?
• What is the GCF of the set #64, 16n^2, 32n#?
• How do you write the reciprocal number of 5?
• Jeanie has a 3/4 yard piece of ribbon. She needs one 3/8 yard piece and one 1/2 yard piece. Can she cut the piece of ribbon into the two smaller pieces? Why?
• How do you find the GCF of #25k, 35j#?
• How do you write 132/100 in a mixed number?
• How do you evaluate the power #2^3#?
• How do you simplify #(4^6)^2 #?
• How do you convert 3.2 tons to pounds?
• How do you solve #\frac { 5} { 8} + \frac { 3} { 2} ( 4- \frac { 1} { 4} ) - \frac { 1} { 8}#?
• What are some acronyms for PEMDAS?
• How do you find all the asymptotes for function #y=(3x^2+2x-1)/(x^2-4 )#?
• How do you determine whether the graph of #y^2+3x=0# is symmetric with respect to the x axis, y axis or neither?
• How do you determine whether the graph of #y^2=(4x^2)/9-4# is symmetric with respect to the x axis, y axis, the line y=x or y=-x, or none of these?
• How do you find the end behavior of #-x^3+3x^2+x-3#?
• How do you find the asymptotes for #(2x^2 - x - 38) / (x^2 - 4)#?
• How do you find the asymptotes for #f(x) = (x^2) / (x^2 + 1)#?
• How do you find the vertical, horizontal and slant asymptotes of: #(3x-2) / (x+1)#?
• How do you find the Vertical, Horizontal, and Oblique Asymptote given #s(t)=(8t)/sin(t)#?
• How do you find vertical, horizontal and oblique asymptotes for #(x^3+1)/(x^2+3x)#?
• How do you find vertical, horizontal and oblique asymptotes for #y = (4x^3 + x^2 + x + 5 )/( x^2 + 3x)#?
• What is a pooled variance?
• What is the mean, mode median and range of 11, 12, 13, 12, 14, 11, 12?
• What is the z-score of sample X, if #n = 81, mu= 43, St. Dev. =90, and E[X] =57#?
• The camera club has five members, and the mathematics club has eight. There is only one member common to both clubs. In how many ways could a committee of four people be formed with at least one member from each club?
• How many permutations are there of the letter in the word baseball?
• How do you evaluate 6p4?
• What is the probability of #X= 6# successes, using the binomial formula?
• A lottery has a $100 000 first prize, a $25 000 second prize, and five $500 third prizes. A total of 50000 tickets are sold. What is the probability of winning a prize in this lottery?
• When a event is reported, the probability that is a negative event is 30%. What is the probability that 3 out of 5 reported events are negative?
• What is the median of 5, 19, 2, 28, 25?
• How do you solve this trigonometric equation?
• What is the frequency of #f(theta)= sin 3 t - cos2 t #?
• How do you evaluate #Sin(pi/2) + 6 cos(pi/3) #?
• How do you find the values of all six trigonometric functions of a right triangle ABC where C is the right angle, given a=9, b=40, c=41?
• How do you express (5*pi)/4 into degree?
• Solve for θ on the interval [90°,180°]:2tanθ +19 = 0?
• Prove that #((cos(33^@))^2-(cos(57^@))^2)/((sin(10.5^@))^2-(sin(34.5^@))^2)= -sqrt2# ?
• A triangle has sides A, B, and C. The angle between sides A and B is #(pi)/3# and the angle between sides B and C is #pi/6#. If side B has a length of 26, what is the area of the triangle?
• How do you write the following in trigonometric form and perform the operation given #(sqrt3+i)(1+i)#?
• A triangle has sides A, B, and C. The angle between sides A and B is #(2pi)/3#. If side C has a length of #32 # and the angle between sides B and C is #pi/12#, what is the length of side A?

Trust HIX Tutor’s Math AI for Reliable Math Solutions

Don’t waste hours slaving over complex equations or confusing mathematical word problems. Math AI Solver is the ultimate solution for completing math assessments quickly and efficiently. Get started now.

• Election 2024
• Entertainment
• Newsletters
• Photography
• AP Buyline Personal Finance
• AP Buyline Shopping
• Press Releases
• Israel-Hamas War
• Russia-Ukraine War
• Global elections
• Asia Pacific
• Latin America
• Middle East
• Delegate Tracker
• AP & Elections
• 2024 Paris Olympic Games
• Auto Racing
• Movie reviews
• Book reviews
• Financial Markets
• Business Highlights
• Financial wellness
• Artificial Intelligence
• Social Media

Kerr says Tatum’s minutes at Paris Olympics come down to a mathematical logjam

Steve Kerr, coach for the United States gestures during a men’s semifinals basketball game against Serbia at Bercy Arena at the 2024 Summer Olympics, Thursday, Aug. 8, 2024, in Paris, France. (AP Photo/Mark J. Terrill)

United States’ Jayson Tatum, right, celebrates after dunking as United States’ LeBron James watches during a men’s basketball game against Brazil at the 2024 Summer Olympics, Tuesday, Aug. 6, 2024, in Paris, France. (AP Photo/Michael Conroy)

United States’ Kevin Durant (7) celebrates after beating Serbia during a men’s semifinal basketball games in the 2024 Summer Olympics, Thursday, Aug. 8, 2024 in Paris, France. (AP Photo/Michael Conroy)

United States’ Jrue Holiday in action during a men’s quarterfinal game against Brazil at Bercy Arena at the 2024 Summer Olympics, Tuesday, Aug. 6, 2024, in Paris, France. (AP Photo/Michael Conroy, Pool)

• Copy Link copied

Follow along for the latest updates from today’s Olympic action , including the gold medal men’s basketball game between the U.S. and France.

PARIS (AP) — Jayson Tatum has not played in two of the five U.S. games at the Paris Olympics, held out of both matchups against Serbia.

And once again, U.S. coach Steve Kerr said Friday that it’s not an indictment of Tatum.

“It’s not what I’m not seeing from Jayson. It’s what I’ve seen from the other guys,” Kerr said. “Like I’ve said many times during this tournament and this last six weeks, it’s just hard to play 11 people, even in an NBA game.”

Being down for most of the game — the U.S. trailed by 17 points in the first half and by 15 late in the third quarter — led to Kerr shortening his rotation in the semifinal victory. Stephen Curry played 33 minutes and LeBron James played 32, the first two instances of a U.S. player logging more than 27 minutes in any game of this tournament.

Part of that was because the second unit, a strength for the Americans in the first four games, never clicked Thursday night. That grouping of Anthony Davis, Kevin Durant, Derrick White, Bam Adebayo and Anthony Edwards played only four minutes together, getting outscored 17-4 while Serbia made all five of its field-goal tries.

Tatum is a star, without question. He agreed to an NBA-record $315 million contract this summer, is a perennial All-NBA pick and now is a champion as well. It also should be noted that Tatum was one of two players to log 23 minutes in the group stage finale against Puerto Rico — and that he’s the only player on the roster not to make a 3-pointer yet in these Olympics.

“It’s not about anything Jayson is doing or not doing,” Kerr said. “It’s just about combinations and the way that group has played together, the way Kevin has filled in since he came back from his injury. It’s just a math problem more than anything.”

5 games, 5 leaders

Through five games, the U.S. has had five different leaders in scoring at these Paris Games. And that makes it tough to say who’ll lead in the gold-medal game against France on Saturday night.

Catch up on the latest from Day 15 of the 2024 Paris Olympics:

• Basketball: Steph Curry’s late barrage seals fifth straight Olympic men’s basketball title , as US beats France.
• Gymnastics: Romanian gymnast Ana Barbosu could replace Jordan Chiles as bronze medalist in floor exercise after a court ruling.
• Soccer: The U.S. women’s soccer team won its fifth Olympic gold medal , and first since 2012, by beating Brazil 1-0.

It’s almost over: What to know about the Paris Olympics closing ceremony .

Follow along with our Olympics medal tracker and list of winners. Here is the Olympic schedule of events.

Kevin Durant scored 23 in the tournament opener against Serbia. Bam Adebayo had 18 against South Sudan, Anthony Edwards had 26 against Puerto Rico, Devin Booker scored 18 against Brazil and Stephen Curry scored 36 in the comeback over Serbia in the semifinals.

Curry shot only three times against Brazil in the quarterfinals.

“It’s whatever the game calls for. I shot three times last game and I wasn’t looking to force it because that’s not what the game called for,” Curry said. “So, that’s the beauty of Team USA and FIBA and this whole experience. Every game, it’s been somebody different. And it’s going to be somebody different, hopefully, with everybody contributing on Saturday.”

Durant has chance at 4-timers club

Kevin Durant is one win away from becoming the first men’s player with four Olympic gold medals. And it’s a fairly short list of Americans with four golds in any event.

Sue Bird and Diana Taurasi each have five gold medals in women’s basketball, while Teresa Edwards, Lisa Leslie, Sylvia Fowles and Tamika Catchings each have four golds.

OLYMPIC PHOTOS : See AP’s top photos from the 2024 Paris games

The rest of the four-time champions in the same event is pretty much a who’s who of U.S. Olympic history.

Swimming icon Michael Phelps has done it in three different events (4x100-meter medley relay, 4x200-meter freestyle relay and 200-meter individual medley).

Others in the four-time, one-event, gold-medal club: swimmers Katie Ledecky (800-meter freestyle) and Ryan Lochte (4x200-meter freestyle relay), sprinter Allyson Felix (4x400-meter relay), discus thrower Al Oerter, long jumper Carl Lewis and shooter Vincent Hancock (skeet).

Celtics can make history

The three members of the NBA champion Boston Celtics on this team — Jayson Tatum, Jrue Holiday and Derrick White — can join a special club if the U.S. beats France for gold on Saturday.

There have been only 12 instances of a player winning an NBA or WNBA championship and an Olympic gold medal in the same calendar year.

Holiday did it once before, winning the NBA title with Milwaukee in 2021 before going to the Tokyo Games and helping the U.S. win gold.

The others on the list: Stefanie Dolson (a 3x3 winner in Tokyo) in 2021, Khris Middleton in 2021, Kyrie Irving in 2016, LeBron James and Tamika Catchings in 2012, Katie Smith in 2008, Sue Bird in 2004, Sheryl Swoopes in 2000, Scottie Pippen in 1992 and 1996, and Michael Jordan in 1992.

AP Summer Olympics: https://apnews.com/hub/2024-paris-olympic-games

An efficient image space branch-reduction-bound algorithm to globally solve generalized fractional programming problems for large-scale real applications

New citation alert added.

This alert has been successfully added and will be sent to:

You will be notified whenever a record that you have chosen has been cited.

To manage your alert preferences, click on the button below.

New Citation Alert!

Please log in to your account

Information & Contributors

Bibliometrics & citations, view options, recommendations, an eigenvalue decomposition based branch-and-bound algorithm for nonconvex quadratic programming problems with convex quadratic constraints.

In this paper, we propose a branch-and-bound algorithm for finding a global optimal solution for a nonconvex quadratic program with convex quadratic constraints (NQPCQC). We first reformulate NQPCQC by adding some nonconvex quadratic constraints induced ...

A branch-and-bound algorithm to globally solve the sum of several linear ratios

In this paper we propose a branch-and-bound algorithm to globally solve the sum of several linear fractional functions over a polytope. For minimizing problem a linear lower bounding function (LLBF) of the objective function is constructed, then a ...

Branch-and-Bound Outer Approximation Algorithm for Sum-of-Ratios Fractional Programs

In this article, a branch and-bound outer approximation algorithm is presented for globally solving a sum-of-ratios fractional programming problem. To solve this problem, the algorithm instead solves an equivalent problem that involves minimizing an ...

Information

Published in.

Elsevier Science Publishers B. V.

Netherlands

Publication History

Author tags.

• Generalized fractional programming problems
• Global optimization
• Two-phase relaxation technique
• Branch-reduction-bound
• Computational complexity
• Research-article

Contributors

Other metrics, bibliometrics, article metrics.

• 0 Total Citations
• 0 Total Downloads
• Downloads (Last 12 months) 0
• Downloads (Last 6 weeks) 0

View options

Login options.

Check if you have access through your login credentials or your institution to get full access on this article.

Full Access

Share this publication link.

Copying failed.

Share on social media

Affiliations, export citations.

• Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
• Download citation
• Copy citation

We are preparing your search results for download ...

We will inform you here when the file is ready.

Your file of search results citations is now ready.

Your search export query has expired. Please try again.